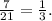Найдите наименьшее положительное значение дроби:

Пошаговое объяснение:

Чтобы дробь достигала минимального значения, числитель должен быть минимален, а знаменатель - максимальным. Заметим, что как в числителе, так и в знаменателе квадратные уравнения относительно a и b, причем в уравнении относительно a, минимальное значение которого нас интересует, коэффициент возле x² больше нуля, следовательно, ветки параболы направлены вверх, и минимальное значение функция принимает в вершине параболы.

В уравнении относительно b ветки параболы направлены вниз, следовательно, максимальное значение достигается так же в вершине параболы.

Вычислим абсциссы вершин парабол по формуле x=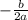, где a и b - коэффициенты перед x² и x соответственно.

Абсцисса вершины параболы для функции относительно a x=.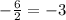

Значение ординаты в этой точке найдём, подставив полученное значение x в уравнение, получим:

y=9-18+16=7

Проделаем то же для уравнения в знаменателе, получим:

x=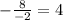

y=5+32-16=21

Минимальное положительное значение дроби: