Найдите наибольшее значение функции x^5 - x^3 - 20x на отрезке [-9; 0]

Ответы

Dilnoza81100 27.09.2020 22:46

Найдем точки экстремума, предварительно вычислив производную функции первого порядка

$f'(x)=\left(x^5-x^3-20x\right)'=5x^4-3x^2-20=0$

Решим как квадратное уравнение относительно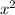 x^2

$D=(-3)^2-4\cdot 5\cdot(-20)=409\\ \\ x^2=\dfrac{3-\sqrt{409}}{2\cdot5}$

Это уравнение решений не имеет, так как левая уравнения положительно, а правая - отрицательно.

$x^2=\dfrac{3+\sqrt{409}}{10}\\ \\ x=\pm\sqrt{\dfrac{3+\sqrt{409}}{10}}$

Только $x=-\sqrt{\dfrac{3+\sqrt{409}}{10}}\in [-9;0]$ , второй корень не удовлетворяет условию.

Найдем наибольшее значение функции на концах отрезка.

$f(-9)=-9^5+9^3+20\cdot9=-58140\\ f(0)=0\\ f\left(-\sqrt{\dfrac{3+\sqrt{409}}{10}}\right)\approx26$

ответ: $\displaystyle \max_{[-9;0]}f(x)=26$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

маринчик18 10.09.2019 03:10

(3000+240) : 10 99: 11x (3х3) 812-398x2 (5050-50)х100 669+425: 5 72: (12х6) х 4...

olyakokos 10.09.2019 03:10

EgorFolt2123121 10.09.2019 03:10

конфетка03031 10.09.2019 03:10

CorrupteD 10.09.2019 03:10

jjrey252 10.09.2019 03:10

Аринка20061 10.09.2019 03:10

AnjelikaM1 10.09.2019 03:10

Ьала 10.09.2019 03:10

Ангелина10волкова120 10.09.2019 03:10