Найдите наибольшее значение функции у=11+24х-2х корень из х

523

Пошаговое объяснение:

Дана функция:

Область определения функции: x≥0 или x∈[0; +∞)

Производная функции

Определим критические точки:

y'=0 ⇔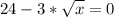 ⇔ ⇔ 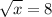x=64.

Рассмотрим знак производной

если 0<x<64, то ;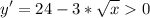

если 64<x, то .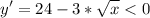

Отсюда на интервале x∈(0; 64) функция строго возрастает, а на интервале x∈(64; +∞) функция строго убывает. Тогда х=64 точка максимума и наибольшее значение функции: