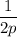Найдите наибольшее значение функции 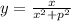
на промежутке
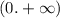
Другие вопросы по теме Математика
Популярные вопросы
- Задания суммативного оценивания За 4 четверть по предмету «Русский язык» (с русским...
1 - Известно, что угол β — это угол преломления луча, выходящего из призмы. Также...
1 - Реши систему уравнений методом подстановки. {3−5(0,2y−2u)=3(3u+2)+2y4(u−3y)−(2u+y)=11−2(2u+y)...
1 - Test. Listening https://yadi.sk/d/qvtHBwOxyOVFog Вы два раза услышите пять высказываний...
3 - ) (-10; -2), (-11; -3), (-10,5; -5), (-11; -7), (-12; -10), (-11; -13), (-13;...
3 - Путешествие алисы. какую загадку хотели отгадать космонавты сегодня уже сдавать....
3 - Найдите длину дуги окружности радиуса 15 см, если ее градусная мера равна 36°.А...
1 - Составьте предложения, используя [to be] going to.Model: I (rent) a boat. – I...
1 - Экожүйелердің өзгеру себебін болжа Экожүйедегі абиотикалық факторларды анықта:Экожүйедегі...
3 - 1) Найти массу осадка, образующегося при взаимодействии 280 г. раствора хлорида...
3
Заметим, что для рассмотрения функции можно считать, что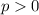 , так как в функцию
, так как в функцию 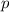 входит в четной степени
входит в четной степени
Найдем производную:
Найдем точки, в которых производная равна нулю:
На промежутке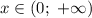 с учетом уточнения
с учетом уточнения 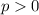 такая точка одна:
такая точка одна:
Найдем точки, в которых производная не существует:
Равенство выполняется при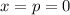 , однако эта точка не попадает в заданный промежуток
, однако эта точка не попадает в заданный промежуток 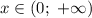
Таким образом, нужно проверить наличие экстремума в точке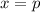 .
.
Найдем знаки производной в точках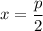 и
и 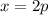 :
:
Значит:
при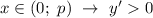
при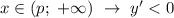
Таким образом, при переходе через точку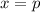 производная меняет знак с "плюса" на "минус". Значит,
производная меняет знак с "плюса" на "минус". Значит, 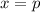 - точка максимума. Найдем значение максимума:
- точка максимума. Найдем значение максимума:
Поскольку заданный промежуток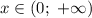 не отрезок, то проверим, что предел при стремлении
не отрезок, то проверим, что предел при стремлении  к границам промежутка не больше полученного максимума:
к границам промежутка не больше полученного максимума:
Оба предела равны 0. Значит,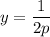 - наибольшее значение функции на заданном промежутке.
- наибольшее значение функции на заданном промежутке.
ответ: