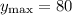Найдите наибольшее значение функции

Другие вопросы по теме Математика
Популярные вопросы
- Как можно назвать по другому слово произведение я пишу сочинения...
3 - Многие считают заботу о здоровье исключительно личным делом человека,...
3 - 5. Выполните сложение, выбирая удобный порядок действий:а) 1888...
1 - в 1.97 первые 3 я зделала...
1 - Где находится уральские горы по отношению к кавказским...
2 - Определите объем кислорода который необходим для взаимодействия...
1 - Эссе на тему моя будущая профессия раскрыть её возможные связи...
1 - Имеет ли для меня значение изучать литературу как для будущего...
2 - Объясните вкратце работу программы, не догоняю в какой строке...
1 - Автомат по разливу молока за 28 сек наполняет 21 пакет.сколько...
2
Найдем производную функции:
Найдем критические точки функции, приравняв производную к нулю:
Общее решение: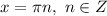
Найдем критические точки, которые входят в интервал![x \in \left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]:](/tpl/images/1359/4472/29934.png)
еслиНайдем значение функции на концах отрезка![\left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]](/tpl/images/1359/4472/7c285.png) и в критической точке
и в критической точке 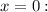
Таким образом,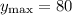
ответ: