1. Математика
  2. найдите корни уравнения(х⁴+1)/(х(х²+1))=41/15​

найдите корни уравнения
(х⁴+1)/(х(х²+1))=41/15​

tvzhanna80 tvzhanna80    1   18.06.2021 00:21    3

Ответы
73487Юлия14271 73487Юлия14271  18.07.2021 00:23

\frac{x^4+1}{x(x^2+1)}=\frac{41}{15}; ОДЗ: x\not= 0;

делим числитель и знаменатель левой части на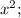 x^2;

\frac{x^2+\frac{1}{x^2}}{x+\frac{1}{x}}=\frac{41}{15};\ 15((x+\frac{1}{x})^2-2)=41(x+\frac{1}{x});\ x+\frac{1}{x}=t;\ 15t^2-30=41t;

15t^2-41t-30=0;\ \left [ {{t=10/3} \atop {t=-3/5}} \right. .

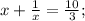
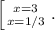
1-й случай. x+\frac{1}{x}=\frac{10}{3};\left [ {{x=3} \atop {x=1/3}} \right. .

2-й случай.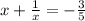 x+\frac{1}{x}=-\frac{3}{5} - здесь решений нет, так как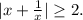 |x+\frac{1}{x}|\ge 2.

ответ:  3;   1/3.

Замечание. В первом случае я уравнение не решал, а просто угадал ответ - ведь 10/3=3+1/3. Других решений быть не может, так как после избавления от знаменателя получается квадратное уравнение, которое больше двух решений иметь не может. Во втором случае, если у Вас сложности с неравенством Коши между средним арифметическим и средним геометрическим, можете спокойно свести все к квадратному уравнению и убедиться в отрицательности дискриминанта.  

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
laparoscopic laparoscopic  25.11.2020 13:51
РАБОТА В ПАРЕ 3Вычисли, записывая в столбик1235 × 2312 541т× 2355 261 × 1752311 × 254073 × 1334 103 × 221ФОТО СТОЛБИКОМ ​...
ksenia87109r675 ksenia87109r675  25.11.2020 13:52
Номер 30,31,32,36 чень заранее...
berezovskatanap09xfx berezovskatanap09xfx  25.11.2020 13:52
D) -12а 13 а + 15 X) 15а +2b — 4-6 -55Ц) 25х2у=3x5yЧ) За — 8x 15а +6хШане 12а НЗЬ 14Щ) — 18-13a 1b H1Ы) 21 4 — — 8 25аЫ) 2а 20Ь 20a +2bБ) Тc—13x +7 x — сЭ) ба — 9Ь — 6xH OЬ —7а —...
Sidoriva Sidoriva  25.11.2020 13:52
БЫСТРЕЕ Довжина Дунаю 2850 км. Яка довжина річки Південний Буг, якщо вона становить 7/25 довжини Дунаю?...
hdhshuuyfftf hdhshuuyfftf  25.11.2020 13:52
Установи соответствие, где m, n, p, q – любые рациональные числа....
mashoklomakina mashoklomakina  25.11.2020 13:52
Прямая а перпендикулярна сторонам АВ и ВС параллелограмма АВСD. Будет ли прямая а перпендикулярна плоскости параллелограмма? Объяснить...
nastena544 nastena544  25.11.2020 13:52
525. Теңдеуді шешіңдер: 1) 12х = 6; 3) 5х + 3 = 8;2) 3x = 12; 4) 4xl + 5 = 17;5) 1,5х1 — 2 = 4;5) 7 – 16x = -5.​...
Марусяняша Марусяняша  25.11.2020 13:52
только что бы было расписано​...
Вовка753 Вовка753  25.11.2020 13:52
в зоомагазине было 7 котят а попугайчиков на 3 больше сколько всего котят и попугайчиков было в магазине​...
zarinadmitrievI zarinadmitrievI  25.11.2020 13:52
Длина прямоугольника 4 см а ширина 2 см найдите переметр​...

Популярные вопросы