Найдите корень уравнения,выраженный натуральным числом: х(х+10)=119; х(х-18)=115: х(х+2)=143.
Другие вопросы по теме Математика
Популярные вопросы
- Вместе с ним в том же направлении выбежал пес шарик 12: 00 петя пошел в соседнею...
3 - Решить уравнение ײ+6×+5=0 ײ+3,5×-2=0...
3 - Найти и доказать принципы детектива из рассказа убийство на улицы морг...
2 - Jane has got a закончить предложения....
3 - Прочитайте.спишите вставляя пропущенные окончания имен прилагательных. весть, дорога,...
2 - Грамматическая основа в предложении: другого шкафа у них нет....
1 - Сделать рассказ о вымирающем животном по примерно 5-6 предложений заранее !...
1 - Масса свинцовой детали составляет 3955гр. каков объём этой детали? плотность свинца...
2 - The worlds a very happy place where every child should laugh and sing and always...
1 - Составить с рациональными числами про вертолёты 6 класс заранее...
2
1) х(х+10)=119
х^2+10х-119=0
х1=(-10+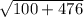 )2=(-10+24)/2=7
)2=(-10+24)/2=7
х2=(-10-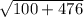 )2=(-10-24)/2=-17
)2=(-10-24)/2=-17
х1=7, х2=-17
ответ. корень равен 7
2) х(х-18)=115
х^2-18х-115=0
х1= (18+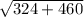 )2=(18+28)/2=46/2=23
)2=(18+28)/2=46/2=23
х2= (18-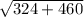 )2=(18-28)/2=-10/2=-5
)2=(18-28)/2=-10/2=-5
ответ. корень равен 23
3) х(х+2)=143
х^2+2х-143=0
х1= (-2+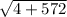 )2=(-2+24)/2=11
)2=(-2+24)/2=11
х2= (-2-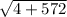 )2=(-2-24)/2=-13
)2=(-2-24)/2=-13
ответ корень равен 11
x²+10x=119
x²+10x-119=0
D=b²-4ac=10²-(-4(1*119))=576
x₁₂=-b±√D/2a=-10±√576/2
x=-17,7
x²-18x=115
x²-18x-115=0
D=b²-4ac=(-18)²-(-4(1*115))=576
x₁₂=-b±√D/2a=18±√784/2
X=-5,23
x²+2x=143
x²+2x-143=0
D=b²-4ac=2²-(-4(1*143))=576
x₁₂=-b±√D/2a=-2±√576/2
x=-13,11