1. Математика
  2. Найдите координаты векторов,

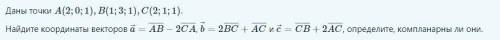
Найдите координаты векторов, определите, компланарны ли они.


Найдите координаты векторов, определите, компланарны ли они.

Hotaru385 Hotaru385    2   02.01.2021 17:17    0

Ответы
karisafedotova2 karisafedotova2  12.02.2021 21:53

\vec{AB} = (-1,\;3,\;0)\\ \vec{BC} = (1,\;-2,\;0)\\ \vec{AC} = (0,\; -1,\; 0)

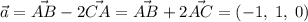Поэтому любая комбинация векторов не выводит за пределы плоскости, уравнение которой легко найти, вычислив нормальный вектор как векторное произведение [\vec{BC},\;\vec{AC}] = \det\left(\begin{array}{ccc}\textbf{i}&\textbf{j}&\textbf{k}\\1&-2&0\\0&-1&0\end{array}\right)=(0,\;0,\;1) - здесь он весьма примитивен. 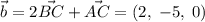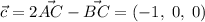Но для систематического подхода давайте проделаем общие выкладки: \vec{a} = \vec{AB}-2\vec{CA}=\vec{AB}+2\vec{AC} = (-1,\;1,\; 0), \vec{b} = 2\vec{BC}+\vec{AC} = (2,\; -5,\;0), \vec{c}=2\vec{AC}-\vec{BC} = (-1,\; 0,\; 0).

Смешанное произведение: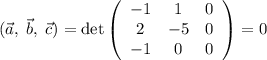 (\vec{a},\; \vec{b},\; \vec{c}) = \det \left(\begin{array}{ccc}-1&1&0\\2&-5&0\\-1&0&0\end{array}\right) = 0, то есть векторы компланарны, что мы и заключили в самом начале.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
aaaaaa251 aaaaaa251  30.04.2020 14:32
На каком расстоянии от начала координат расположена точка В (2; -4; -4)​...
switt1q switt1q  30.04.2020 14:31
Знайдіть висоту прямокутного паралелипіпеда, якщо площа його основи дорівнює 18,5см,а обєм 7,4см3...
Hasky12 Hasky12  30.04.2020 14:31
Пусть h-расстояние от прямой d до центра сферы G(O,R).Определите взаимное расположение прямой d и сферы,если:h=8 см,R=9 см...
Daann4ik Daann4ik  30.04.2020 14:31
Привет всем, нужна в решении таких примеров 5 ц 19 кг : 1 ц 73 кг 9 м 5 см 4 мм :18...
д2и0а0н6а д2и0а0н6а  30.04.2020 14:30
7+7 77777+77777 6666+6666​...
AnnaKaramelka6684 AnnaKaramelka6684  30.04.2020 14:30
решить Уро жайность картофеля у двух фермеров одинаковая.Они собрали вместе 450т. Какова урожаиность картофеля (т/га) если у одного из них было засажено 8 га, а...
kanony kanony  30.04.2020 14:30
1.Запишите в виде десятичной дроби ( нужно делить на 100) 5%; 24%; 156% 2.Запишите в процентах ( нужно умножать на 100) 0,57 0,07 3,59 3. Площадь поля равна 300...
aykmuradyan20 aykmuradyan20  30.04.2020 14:31
Одне число в 1,5 разів менше від другого. Якщо до першого числа додати 3,7, а від другого відняти 5,3, то одержимо однакові результати. Знайдіть ці числа​...
Виола122006 Виола122006  30.04.2020 14:31
27346+9875=... 384058+615942=... 16620-9064=... 600000-39482=... 74890+38315-25548=... 20305-(7484+6359)=......
стас488 стас488  30.04.2020 14:30
Скласти зведене квадратне рівняння з коренями 2 і 4...

Популярные вопросы