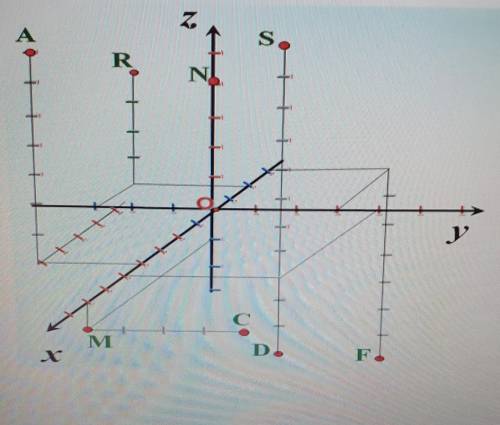
Найдите координаты точек:A,C,D,F,M,N,R,S​

Для начала определим координаты точек, которые даны на рисунке.

Точка A находится на пересечении оси абсцисс (OX) и прямой, проходящей через точку (0,2) и имеющей наклон k=-1. Поэтому мы можем записать уравнение этой прямой в виде y = -x + b. Для нахождения b подставляем координаты точки A: 2 = -0 + b. Отсюда b = 2. Таким образом, уравнение прямой, на которой лежит точка A, имеет вид y = -x + 2. Зная это уравнение, мы можем найти координаты точки A через подстановку её координат (x,y) в это уравнение.

1. Заметим, что прямая, на которой лежит точка C, параллельна оси абсцисс, так как её угловой коэффициент равен 0. Это означает, что x-координата точки C равна 0. Осталось найти y-координату. Так как точка C находится на прямой, проходящей через точку (0,2) и имеющей наклон k=-1, мы можем подставить x=0 в уравнение этой прямой, чтобы найти y-координату точки C. Получаем y = -0 + 2 = 2.

Таким образом, координаты точки C равны (0,2).

2. Точка D находится на пересечении оси абсцисс и перпендикулярной прямой, проходящей через точку (0,2). Так как эта прямая перпендикулярна прямой, на которой лежит точка A, то её угловой коэффициент равен -1/(-1) = 1. Теперь мы можем записать уравнение прямой, на которой лежит точка D, в виде y = x + b. Подставим координаты точки (0,2) в это уравнение: 2 = 0 + b. Отсюда b = 2. Таким образом, уравнение прямой, на которой лежит точка D, имеет вид y = x + 2. Зная это уравнение, мы можем найти координаты точки D через подстановку её координат в это уравнение.

Таким образом, координаты точки D равны (x,y).

3. Точка F находится на пересечении оси абсцисс и перпендикулярной прямой, проходящей через точку (0,2). Так как эта прямая перпендикулярна прямой, на которой лежит точка A, то её угловой коэффициент равен -1/(-1) = 1. Теперь мы можем записать уравнение прямой, на которой лежит точка F, в виде y = x + b. Подставим координаты точки (0,2) в это уравнение: 2 = 0 + b. Отсюда b = 2. Таким образом, уравнение прямой, на которой лежит точка F, имеет вид y = x + 2. Зная это уравнение, мы можем найти координаты точки F через подстановку её координат в это уравнение.

Таким образом, координаты точки F равны (x,y).

4. Точку M можно найти как середину отрезка AB. Для этого нужно найти среднюю арифметическую для x- и y-координат точек A и B. Координаты точек A и B: A(1,1) и B(7,1). x-координаты точек A и B равны 1 и 7 соответственно. Среднюю арифметическую для x-координат найдём по формуле (x1 + x2) / 2. Подставим значения x-координат A и B в формулу и получим (1 + 7) / 2 = 8 / 2 = 4. Таким образом, x-координата точки M равна 4. Аналогично, y-координаты точек A и B равны 1 и 1 соответственно, а следовательно y-координата точки M также равна 1.

Таким образом, координаты точки M равны (4,1).

5. Чтобы найти координаты точки N, найдём точку E, которая является серединой отрезка CD. Для этого нужно найти среднюю арифметическую для x- и y-координат точек C и D. Координаты точек C и D: C(0,2) и D(x,y). x-координаты точек C и D равны 0 и x соответственно. Среднюю арифметическую для x-координат найдём по формуле (x1 + x2) / 2. Подставим значения x-координат C и D в формулу и получим (0 + x) / 2 = x / 2. Таким образом, x-координата точки E равна x / 2. Аналогично, y-координаты точек C и D равны 2 и y соответственно, а следовательно y-координата точки E также равна y / 2.

Таким образом, координаты точки E равны (x / 2, y / 2).

Теперь заметим, что прямая, на которой лежат точки M и N, проходит через точку F и имеет наклон k=1, так как эта прямая перпендикулярна прямой, на которой лежат точки C и D. Поэтому уравнение этой прямой можно записать в виде y = x + b. Подставим координаты точки F(xF, yF) в это уравнение: yF = xF + b. Также, заметим, что точка M(xM, yM) лежит на этой прямой, поэтому мы можем также записать yM = xM + b.

Из этих двух уравнений, мы можем найти b. Воспользуемся уравнением yF = xF + b и подставим в него координаты точки F: 2 = xF + b. Отсюда b = 2 - xF. Теперь заменим b в уравнении yM = xM + b и получим yM = xM + (2 - xF).

Таким образом, координаты точки M равны (4,1) и координаты точки F равны (xF, yF).

Подставим xM и yM в уравнение yF = xF + b: 2 = xF + (2 - 4). Упростим это уравнение: 2 = xF - 2. Перенесём -2 на другую сторону и получим xF = 2 + 2 = 4. Теперь заменим xF в уравнении yM = xM + (2 - xF) и получим yM = xM + (2 - 4). Упростим это уравнение: yM = xM - 2. Таким образом, координаты точки F равны (4,1 - 2) = (4,-1).

Таким образом, координаты точки N равны ((x/2), (y/2)) = ((4/2),(-1/2)) = (2,-1/2).

6. Точку R можно найти как середину отрезка FM. Для этого нужно найти среднюю арифметическую для x- и y-координат точек F и M. Координаты точек F и M: F(4,-1) и M(4,1). x-координаты точек F и M равны 4 и 4 соответственно. Среднюю арифметическую для x-координат найдём по формуле (x1 + x2) / 2. Подставим значения x-координат F и M в формулу и получим (4 + 4) / 2 = 8 / 2 = 4. Таким образом, x-координата точки R равна 4. Аналогично, y-координаты точек F и M равны -1 и 1 соответственно, а следовательно y-координата точки R также равна 0.

Таким образом, координаты точки R равны (4,0).

7. Точку S можно найти как середину отрезка DE. Для этого нужно найти среднюю арифметическую для x- и y-координат точек D и E. Координаты точек D и E: D(x,y) и E(x/2,y/2). x-координаты точек D и E равны x и x/2 соответственно. Среднюю арифметическую для x-координат найдём по формуле (x1 + x2) / 2. Подставим значения x-координат D и E в формулу и получим (x + x/2) / 2 = (2x + x) / 2 = 3x / 2. Таким образом, x-координата точки S равна 3x / 2. Аналогично, y-координаты точек D и E равны y и y/2 соответственно, а следовательно y-координата точки S также равна 3y / 2.

Таким образом, координаты точки S равны (3x / 2, 3y / 2).

Осталось только найти x и y для точки S. Заметим, что точка S лежит на прямой, проходящей через точки C и D, так как эта прямая перпендикулярна прямой, на которой лежит точка M (и F). Поэтому уравнение этой прямой можно записать в виде y = kx + b. Подставим координаты точки C(xC, yC) в это уравнение: yC = kxC + b. Также, заметим, что точка D(xD, yD) лежит на этой прямой, поэтому мы можем также записать yD = kxD + b.

Из этих двух уравнений, мы можем найти b. Воспользуемся уравнением yC = kxC + b и подставим в него координаты точки C: 2 = kx * 0 + b. Отсюда b = 2. Теперь заменим b в уравнении yD = kxD + b и получим yD = kxD + 2.

Таким образом, координаты точки C равны (0,2) и координаты точки D равны (x,y).

Подставим yC и yD в уравнение yD = kxD + 2: yD = kxD + 2. Упростим это уравнение: yD = kxD + 2. Таким образом, координаты точки D равны (xD, kxD + 2).

Для нахождения xD воспользуемся уравнением углового коэффициента, которое равно k = (yD - yC) / (xD - xC). Заменим в этом уравнении yD и yC на соответствующие значения: k = (kxD + 2 - 2) / (xD - 0). Упростим это уравнение: k = kxD / xD. Перенесём xD на другую сторону и получим kxD = k * xD. Теперь разделим обе части на k и получим xD = kxD / k. Подставим в это уравнение значения углового коэффициента k = 1 и xD = x и получим x = kx / k = x.

Таким образом, координаты точки D равны (x, kxD + 2) = (x, x + 2).

Теперь осталось только подставить в эти уравнения значения координат точки C и решить систему уравнений, чтобы найти x и y для точки D. Подставим xC = 0 и yC = 2 в уравнение y = kx + b: 2 = k * 0 + b. Отсюда b = 2. Теперь заменим b в уравнении y = kx + b и получим y = k * x + 2. Подставим k = 1 в это уравнение и упростим его: y = x + 2. Таким образом, координаты точки D равны (x, x + 2).

Таким образом, координаты точки D равны (x, x + 2).

Я надеюсь, что эти подробные шаги и объяснения помогут вам понять, как найти координаты всех указанных точек на рисунке. Если у вас есть ещё вопросы, не стесняйтесь задавать их!