Найдите количество всех пятизначных натуральных чисел, имеющих ровно две нечетные цифры и три четные цифры.

Всего 5 чётных цифр и 5 нечётных.

Разместить 3 чётных цифры на 5 местах можно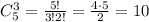

1) XXX**

2) XX*X*

3) XX**X

4) X*XX*

5) X*X*X

6) X**XX

7) *XXX*

8) *XX*X

9) *X*XX

10) **XXX

X - чётная цифра, * - нечётная.

В первых 6 случаях вместо X может стоять чётная цифра, отличная от 0, т.к. число пятизначное. Чисел видов 1-6 будет 4*5*5*5*5 = 2500 каждого вида, всего 2500*6 = 15000 чисел.

Чисел видов 7-10 будет 5*5*5*5*5 = 3125 каждого вида. Всего 3125*4 = 12500 чисел.

Всего пятизначных чисел, имеющих ровно две нечетные цифры и три четные цифры, будет 15000+12500 = 27500.