Найдите интеграл ∫(x-x^-2)dx
Другие вопросы по теме Математика
Популярные вопросы
- как называется геометрическая фигура ,образованная тремя отрезками ,которые...
2 - Таблица по истории 6 класс17 параграф...
3 - 3) какие материки, какими океанами омываются 4) главные реки ( название, место...
3 - описание вегетативного размножения растения...
2 - Вставить пропущенную букву tee-h...
1 - Составить уравнение прямой, проход. ч\з т.А(1;5) паралельно прямой 2х+у-4=0...
1 - Скільки теплоти виділиться при повному згорянні 5 л спирту?...
2 - Обчислити масові частки валетностів у ортопосфорній кислоті H3PO4...
3 - Вычыслите отношение 18/48 30/65 1000:125 96:64 50 см к 2 м 20 мин к 2 часам...
3 - 2 аргумента к тезису»разборчивый почерк не только наше но и общественное дело»и...
1
Использованные формулы:
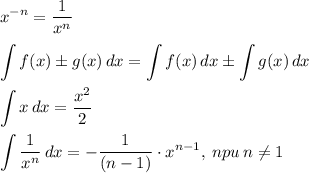
ответ: