Найдите f '(0) , если f (x) = x(x -1)...(x -100) .
С объяснением и подробным поиском производной
Другие вопросы по теме Математика
Популярные вопросы
- Выразить в градусах 1) угол a = 4п/45 2)угол a = 49п/36 3)угол a = 5п/36 4)угол...
1 - Какое произведение относится к жанру оды? а) «вольга и микула селянинович»,...
1 - Решите систему уравнений: у=2х+5 2х+3у=31...
3 - Верны ли следующие высказывания? а. серная кислота - двухосновная б. оксид...
1 - Сравни. 35см 6дм -15см. 72л - 28л. 58дм .. 7м - 12дм...
3 - Решите систему: x+y=пи/2 sin(x-y)=1...
2 - Напишите небольшое сочинение об одном из стран востока или африки в новое время...
3 - 1. нормы семейного права применяются 1) если необходимо определить размеры...
2 - 2.какую массу воды можно нагреть на 30с, сообщив ей 378 кдж количества теплоты?...
2 - Составьте рассказ на тему какой сегодня день? описание умоляю...
2
Пошаговое объяснение:
Используем формулу дифференцирования произведения:
Остается подставить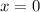 :
: