Найдите экстремумы функции (фото . даю 5 звёзд за ответ.
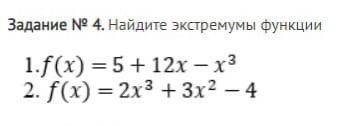
Другие вопросы по теме Математика
Популярные вопросы
- Найдите слова в которых есть нулевое окончание пони,обезьяна,слон,лев,кенгуру,попугай...
3 - Дайте название mg(oh)2 h3po4 nahso4 (znoh)cl kno3lico3 na3[alfu] nh4fe(so4)2...
2 - Прадоужиная казка пра апострау и мякки знак...
1 - Определение слова человек по обществознанию...
2 - Одна вторая а плюс три четвертых а при а =8...
3 - Нужно сочинить сказку про страну морфологию! или другими словами, про...
2 - Стихотворение в котором есть кукование кукушки, кваканье лягушки...
3 - найти: 0,12% от числа 353 101% от числа 15 1,3% от числа 271 103% от...
2 - Нужно расставить степени окисления и валентность у следующих элементов:...
1 - Как нужно писать не с наречиями в словах данных предложений? 1.солнце...
2
Відповідь:
Покрокове пояснення:
1. f(x)=5+12x-x^2
f'(x)=12-2x
f'(x)=0 → 12-2x=0 →x=6
f(6)=5+72-36=41
Максимальное значение функции при х=6
2 f(x)=2х^3+3х^2-4
f'(x)=6х^2+6х
f'(x)=0 → 6х^2+6х=0
х(х+1)=0 →х=0 или х=-1
f(0)= -4; f(-1)=-2+3-4= -3
Имеем локальную точку минимума и максимума
Точки экстремума функции х=0 и х=-1