Найдите двузначное число, у которого число десятков больше числа единиц на 5, а сумма удвоенного числа десятков и числа единиц равна 13.
можете составить систему и решить? ?
Другие вопросы по теме Математика
Популярные вопросы
- Нужно вписать Епитеты з байки Щука...
2 - Укажіть назву держави васалом якої визнав себе Данило Романович...
1 - Зробити інфографіку Айзека АзімоваНа йакомусь сайті та відіслати...
2 - Поставить by ,in,on by train on my magic carpet...
2 - выполнить тест по информатике 1. Перед вами слова, которые встречаются...
1 - При каких значениях b значения двучлена 11b+5 меньше значений...
3 - 1. Что такое отправление?, 2. Алгоритм действий при пищевых отравлениях?,...
1 - У чому полягає небезпека різних видів ерозії грунтів...
1 - Task 2: translate into English using Passive Voice 1.Яблоки съели...
1 - Для чего автор, оставляя Ассоль на едине с природой всё подробно...
2
ответ: 61 .
Представим искомое число в виде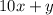 , где
, где  - число десятков, а
- число десятков, а 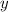 - число единиц.
- число единиц.
Поэтому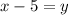 или
или 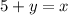 .
.
И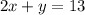 (сумма удвоенного числа десятков и числа единиц равна 13).
(сумма удвоенного числа десятков и числа единиц равна 13).
Имеем систему уравнений (решим ее методом подстановки):
Тогда искомое число - это 61.