Найдите дробь с наименьшими возможными натуральными числителем и знаменателем, которая с точностью не менее 0.01 равна квадратному корню из 5.
Другие вопросы по теме Математика
Популярные вопросы
- Дано: р1=200КПа р2=150КПа V1=10л найти: T1;T2;V2=?...
3 - У рівнобічній трапеції один з кутів 60 °, бічна сторона дорівнює 24...
3 - Будь які числа m і n задовільняють рівність (на фото рівність). Яких...
2 - Берлинская стена строилась в ходе 1 2 берлинского кризиса 2 1 берлинского...
3 - с литературой Укажите этимологию следующих имен в новелле: Натанаэль,...
3 - Для какого возраста подходит роман Эмили Бронте Грозовой перевал ?...
2 - В таблице приведены запросы и количество найденных по ним страниц...
1 - Посчитай, сколько прилагательных в предложении. Запиши число без точки...
3 - Выберите ряд, в котором все слова образованы только суффиксальным...
1 - Мой друг кинул пить до 11 числа, лечится?...
2
Пошаговое объяснение:
Так как искомая дробь отличается от √5 максимум на 0,01, то она лежит в промежутке
Оценим √5: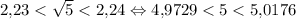 — верно. Тогда
— верно. Тогда
Последовательно переберём натуральные n. m — натуральное число, поэтому между числами 2,22n и 2,25n должно находиться хотя бы одно натуральное число.
n = 1 — 2,22 < m < 2,25 — не подходит;
n = 2 — 4,44 < m < 4,5 — не подходит;
n = 3 — 6,66 < m < 6,75 — не подходит;
n = 4 — 8,88 < m < 9 — не подходит;
n = 5 — 11,1 < m < 11,25 — не подходит;
n = 6 — 13,32 < m < 13,5 — не подходит;
n = 7 — 15,54 < m < 15,75 — не подходит;
n = 8 — 17,76 < m < 18 — не подходит;
n = 9 — 19,98 < m < 20,25 — существует m = 20.
Проверим дробь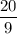 :
:
Неравенство не выполняется, значит, дробь не подходит.
n = 10 — 22,2 < m < 22,5 — не подходит;
n = 11 — 24,42 < m < 24,75 — не подходит;
n = 12 — 26,64 < m < 27 — не подходит;
n = 13 — 28,86 < m < 29,25 — существует m = 29.
Проверим дробь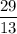 :
:
Значит, данная дробь нам подходит.