Найдите длину высоты, опущенной из вершины B треугольника, построенного на векторах AB = m - 3n и AC = m + n, если длина вектора m = 3, а вектора n = 2 угол между m и n = 60 градусов
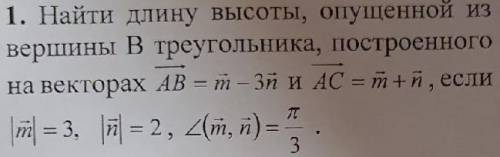
Другие вопросы по теме Математика
Популярные вопросы
- Дополните вопросы 15 1. james works hard at school, he? 2. he...
1 - (21995+406*192)*7-27755: 7= по действиям...
3 - Объясните по пунктам: 1,2, как происходит процесс почвенного...
3 - Примеры подвигов наших солдат совершенных в годы вов кратко...
1 - Выполните возведение в степень 1) (a+2b)^3 2) (x-3y)^3 3) (2m-3n)^3...
3 - Какие из предложеных веществ могут взаимодействовать с водою...
1 - Отцените наиболее улачные , на ваш взгляд сочетание природных...
2 - Запишите произведение в виде многочлена: 1) (а+2)(а+3); 2) 3с^3(2с^3-5)....
2 - Ждим хочет найти друзей по переписке. ему рассказать осебе. закончи...
2 - Над чем смеётся антон павлович чехов в рассказе толстый и тонкий?...
1
У нас есть треугольник ABC, где AB = m - 3n и AC = m + n. Мы хотим найти длину высоты, опущенной из вершины B.
По определению, высота опущенная из вершины B перпендикулярна стороне AC и проходит через вершину B. Обозначим эту высоту как BH, где H - точка пересечения высоты и стороны AC.
Чтобы найти длину высоты BH, нам сначала нужно найти точку H.
Давайте начнем с нахождения точки H. Заметим, что треугольник ABC - это треугольник, построенный на векторах AB и AC. Поэтому мы можем записать вектор AC как сумму векторов AB и BC:
AC = AB + BC.
Имея это, мы можем записать вектор BC как разность векторов AC и AB:
BC = AC - AB.
Заменим векторы AB и AC на их значения:
BC = (m + n) - (m - 3n).
Раскроем скобки:
BC = m + n - m + 3n.
Упростим это:
BC = 4n + 2m.
Теперь, когда у нас есть вектор BC, мы можем использовать его для нахождения точки H. Точка H будет такой точкой на стороне AC, что вектор AH параллелен вектору BC.
Определение параллельности векторов гласит, что если два вектора параллельны, то их косинусы углов равны.
Поэтому мы можем записать следующее:
AH/BC = cos(угол BAH).
Нам дано, что угол между векторами m и n равен 60 градусов, это значит, что косинус этого угла равен 1/2.
Подставим все значения:
AH/(4n + 2m) = 1/2.
Теперь, чтобы найти длину высоты BH, нам нужно найти длину вектора AH. Для этого мы можем использовать формулу длины вектора:
|AH| = sqrt(AH·AH).
Нам дано, что длина вектора m равна 3, а вектора n - 2. В этом случае, мы можем записать вектор AH следующим образом:
AH = (3 - kn), где k - коэффициент масштабирования.
Мы можем подставить это значение в формулу для длины вектора:
|AH| = sqrt((3 - kn)·(3 - kn)).
Теперь, чтобы упростить это, мы можем раскрыть скобки и сгруппировать члены:
|AH| = sqrt(9 - 6kn + k^2n^2).
Заметим, что k^2n^2 - это произведение двух скаляров (квадрат коэффициента масштабирования и квадрата длины вектора n), поэтому мы можем записать его как k^2·n^2.
Теперь у нас есть следующее:
|AH| = sqrt(9 - 6kn + k^2·n^2).
Мы также знаем, что AH/(4n + 2m) = 1/2.
Подставим значение AH в это уравнение:
sqrt(9 - 6kn + k^2·n^2)/(4n + 2m) = 1/2.
Теперь возведем обе части уравнения в квадрат, чтобы избавиться от корня:
(9 - 6kn + k^2·n^2)/(4n + 2m)^2 = 1/4.
Теперь у нас есть квадратное уравнение относительно k. Выполним перемножение на обе стороны уравнения, чтобы избавиться от знаменателя:
4(9 - 6kn + k^2·n^2) = (4n + 2m)^2.
Теперь раскроем скобки и сгруппируем члены:
36 - 24kn + 4k^2·n^2 = 16n^2 + 16mn + 4m^2.
Перенесем все члены в одну сторону уравнения:
4k^2·n^2 - 24kn + (36 - 16n^2 - 16mn - 4m^2) = 0.
Для решения этого уравнения относительно k, нам понадобится использовать квадратную формулу:
k = (-b ± sqrt(b^2 - 4ac))/(2a).
Здесь a = 4n^2, b = -24n и c = 36 - 16n^2 - 16mn - 4m^2.
Подставляя эти значения в формулу, получаем:
k = (-(-24n) ± sqrt((-24n)^2 - 4·4n^2·(36 - 16n^2 - 16mn - 4m^2)))/(2·4n^2).
Теперь решим квадратное уравнение для k. Нам понадобятся значения m и n:
m = 3 и n = 2.
Подставим эти значения:
k = (24n ± sqrt((24n)^2 - 4·4n^2·(36 - 16n^2 - 16mn - 4m^2)))/(2·4n^2).
k = (24·2 ± sqrt((24·2)^2 - 4·4·2^2·(36 - 16·2^2 - 16·2·3 - 4·3^2)))/(2·4·2^2).
Теперь мы можем вычислить два возможных значения k и затем использовать их для нахождения длины высоты BH.
После нахождения значений k, мы можем подставить их в формулу для длины вектора AH:
|AH| = sqrt(9 - 6kn + k^2·n^2).
Таким образом, пошагово решив это уравнение, мы сможем найти длину высоты BH.