Найдите длину прямоугольника,ширина которого 6,а диагональ 2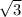 ,но с решением !
,но с решением !
Другие вопросы по теме Математика
Популярные вопросы
- сөзжұмбақтағы жауап сөздерге сұрақ құрастырыңдар.дарбаза, қияр,...
2 - Українська мова 9 клас караман 132вправа...
2 - Даны три числа: А= 100112, В= 18*10, С= 23*10. Переведите числа...
3 - найти ошибки и исправить их...
2 - Какие кнопки калькулятора и в какой последовательности нужно нажимать,...
3 - Как можно применять датчик цвета? Сколько режимов есть у датчика...
1 - При расширений пара какие виды енергии превращается ?...
3 - У землі есть магнитное поле?...
2 - Стихотворный размер строк Не мешай мне жить и так не сладко...
1 - Эссе на тему ТРУДОЛЮБИЕ 5 ПРЕДЛОЖЕНИЙ...
1
(см. объяснение)
Пошаговое объяснение:
Так как диагональ лежит против прямого угла, то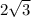 должна быть наибольшей стороной треугольника. Однако
должна быть наибольшей стороной треугольника. Однако 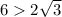 , поэтому такого прямоугольника не существует.
, поэтому такого прямоугольника не существует.
Задание выполнено!
Комментарий:
Можно было решать задачу иначе. Прямоугольник существует только, если выполняется равенство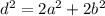 , где
, где 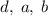 - это диагональ и боковые стороны соответственно. Выполним подстановку данных из условия:
- это диагональ и боковые стороны соответственно. Выполним подстановку данных из условия: 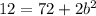 . Получили аналогичный результат.
. Получили аналогичный результат.
Диагональ прямоугольника разбивает его на два равных прямоугольных треугольника .
В этих треугольниках диагональ является гипотенузой, а катеты - это длина и ширина исходного прямоугольника .
Применим теорему Пифагора .
Квадрат диагонали не может получится отрицательным ⇒ в условии допущена ошибка .