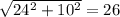Найдите диагональ прямоугольника, стороны которого равны 24 см и 10 см

Пошаговое объяснение:

Дан прямоугольник  ABCD.

В этом прямоугольнике проведена диагональ.

Пусть это диагональ BD.

10 и 24

Следует найти длину диагонали AC.

Пусть известные стороны данного прямоугольника - это стороны a и b или AB и AD.

При этом диагональ, проведенная в прямоугольнике, - это сторона c или BD.

Рассмотрим треугольник ABD.

Так как это прямоугольный треугольник, то найдём его гипотенузу по теореме Пифагора.

Так как по этой теореме в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов, то запишем.

Сторона BD - это и гипотенуза треугольника ABD.

Теперь запишем.

BD² = AB² + AD².

Теперь подставим в данную формулу значения AB и AD, 10 см и 24 см.

BD² = 10² + 24².

BD² = 100 + 576.

BD² = 676.

BD² = 26².

BD = 26(см).

26

Пошаговое объяснение

стороны прямоугольника + диагональ= прямоугольный треугольник

дигональ - это гипотенуза,