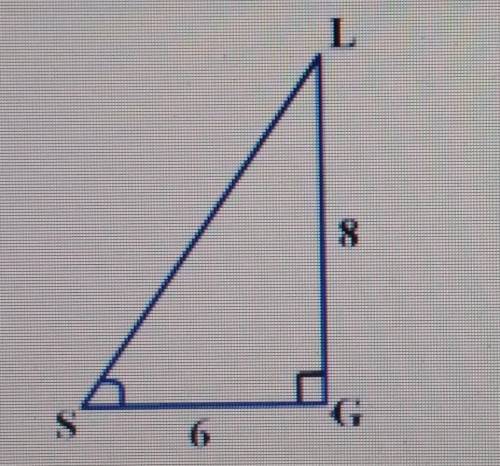
Найдите cos угла S в треугольнике GSL. ответ запишите в виде целого числа или конечной десятичной дроби.​

Для решения данной задачи нам понадобятся знания о тригонометрии и основных свойствах треугольников.

В данной задаче нам нужно найти cos угла S в треугольнике GSL. Для этого нам понадобится использовать определение cos (косинуса) угла в правильном треугольнике.

Правильный треугольник – это треугольник, у которого все стороны равны между собой.

В треугольнике GSL нам известны две стороны: GS и GL. Мы можем воспользоваться теоремой косинусов, чтобы найти третью сторону LS. Теорема косинусов гласит:

c^2 = a^2 + b^2 - 2ab * cos(C),

где c – третья сторона треугольника, a и b – две известные стороны, C – угол между этими сторонами.

Применяя эту формулу к треугольнику GSL, мы получаем:

LS^2 = GS^2 + GL^2 - 2 * GS * GL * cos(S).

Теперь мы можем решить уравнение относительно cos(S):

cos(S) = (GS^2 + GL^2 - LS^2) / (2 * GS * GL).

Для дальнейших вычислений нам нужны значения сторон GS, GL и LS. Мы можем использовать данные из задания для их нахождения.

Из условия задачи нам дано, что GS = 10 и GL = 8.

Остается найти сторону LS. Для этого мы можем применить теорему Пифагора к прямоугольному треугольнику LGS:

LS^2 = GS^2 + GL^2.

Подставим известные значения и найдем LS:

LS^2 = 10^2 + 8^2,
LS^2 = 100 + 64,
LS^2 = 164.

Теперь, когда у нас есть значения GS, GL и LS, мы можем продолжить наше вычисление для нахождение cos(S):

cos(S) = (GS^2 + GL^2 - LS^2) / (2 * GS * GL),
cos(S) = (10^2 + 8^2 - 164) / (2 * 10 * 8),
cos(S) = (100 + 64 - 164) / (2 * 10 * 8),
cos(S) = 0 / 160,
cos(S) = 0.

Таким образом, cos угла S в треугольнике GSL равен 0. Ответ в виде целого числа.