Найдите число целых решений неравенства. С поэтапным решением умоляю надо понять как решить. Заранее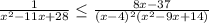
Другие вопросы по теме Математика
Популярные вопросы
- ответе на во как вы поняли заключительные слова Кладовой солнца: А многие до...
3 - Что из перечисленного относится к результатам внешней политики царя Алексея...
3 - Найдите среднее арифметичисое 4 7 6 1 2 8 9 11...
2 - Написать первые 70 чисел 18-ой системы счисления...
2 - Составьте схему политическое управление в Новгороде...
1 - Масса 1см³ стали равна 7,9грамм. Рассчитай массу детали из стали объёмом 4,4см³...
1 - А) Как называется закономерный и последовательный процесс смены сообществ на...
2 - Согласно Марксу, отчуждение это…1)процесс превращения деятельности человека...
2 - найти фразиологизмы .. ДАМ ЗА ЗАДАНИЕ...
2 - Subject of the active sentenc becomes object in the passive sentence (or is...
3
x∈(2;7) ∪ (7;9]
целые: 3, 4, 5, 6, 8, 9
Пошаговое объяснение:
1/(x²-11x+28)≤(8x-37)/((x-4)²(x²-9x+14));
раскладываем квадратные трехчлены на множители:
а)x²-11x+28=0; D=121-4*28=9; x₁₂=0,5(11±3); x₁=7; x₂=4;
x²-11x+28=(x-7)(x-4);
b)x²-9x+14=0; D=81-56=25; x₁₂=0,5(9±5); x₁=7; x₂=2;
x²-9x+14=(x-7)(x-2);
записываем заново, ищем общий знаменатель, приводим подобные, переносим все в левую часть:
1/[(x-7)(x-4)]≤(8x-37)/[(x-4)²(x-7)(x-2)];
1/[(x-7)(x-4)]-(8x-37)/[(x-4)²(x-7)(x-2)]≤0;
[(x-4)(x-2)]-(8x-37)]/[(x-4)²(x-7)(x-2)]≤0;
[x²-2x-4x+8-8x+37]/[(x-4)²(x-7)(x-2)]≤0;
[x²-14x+45]/[(x-4)²(x-7)(x-2)]≤0;
опять раскладываем на множители:
x²-14x+45=0; D=14²-4*45=16; x₁₂=0,5(14±4); x₁=9; x₂=5;
x²-14x+45=(x-9)(x-5);
плучаем вот такое неравенство:
(x-9)(x-5)/[(x-4)²(x-7)(x-2)]≤0;
дробь меньше или равна 0 когда числитель и знаменатель имеют разные знаки:
1. числитель больше или равен 0, а знаменатель меньше 0
2. числитель меньше или равен 0, а знаменатель больше 0
1. числитель ≥0
(x-9)(x-5)≥0; x≥9; x≥5; x∈[9;+∞);
x≤9; x≤5; x∈(-∞;5];
x∈(-∞;5]∪[9;+∞);
1. знаменатель <0 (не равен!)
(x-4)²(x-7)(x-2)<0; (x-4)²>0; (x-7)>0; (x-2)<0
x>2; x>7; x<2; x∈∅;
(x-4)²>0; (x-7)<0; (x-2)>0;
x>2; x<7; x>2; x∈(2;7)
x∈(-∞;5]∪[9;+∞)∩(2;7);
x∈(2;7)
2. числитель ≤0
(x-9)(x-5)≤0; x≥9; x≤5; x∈∅;
x≤9; x≥5; x∈[5;9];
x∈[5;9];
2.знаменатель >0
(x-4)²(x-7)(x-2)>0; (x-4)²>0; (x-7)>0; (x-2)>0
x>2; x>7; x>2; x∈[7;+∞);
(x-4)²<0; (x-7)<0; (x-2)<0;
x∈∅; x<7; x<2; x∈∅
x∈[5;9] ∩ [7;+∞)
x∈[7;9]
x∈(2;7) ∪ [7;9]; (число 7 не входит!)
x∈(2;7) ∪ (7;9]