Найдите четырёхзначное число, у которого максимальный делитель в 77 раз больше минимального. Максимальный делитель отличен от самого числа, минимальный отличен от 1.

например, это число 3773.

Разложение числа на множители:

Максимальный делитель, отличный от самого числа: .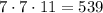

Минимальный делитель, отличный от единицы: .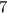

И: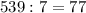 , все сходится!

Если искомое число делится на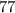 , то его минимальный делитель, отличный от единицы, - хотя бы 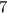(так как 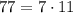). И тогда нужно сделать так, чтобы в искомом числе максимальный делитель, отличный от самого числа, был бы равен 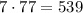. И естественно предположить, что искомое число - это, например, .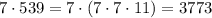