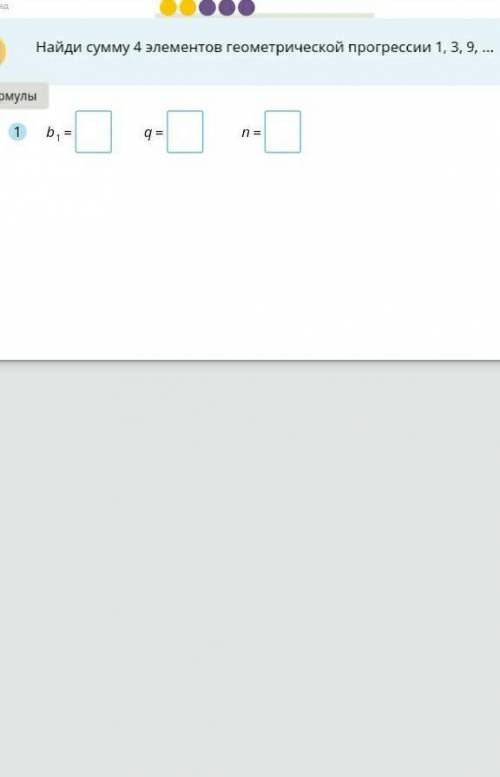
Найди сумму 4 элементов геометрической прогрессии 1, 3 , 9 ...​

сумма 4 элементов прогрессии 40

Пошаговое объяснение:

b1=1 q=3 n=27

Сумма 1+3+9+27=40

Чтобы найти сумму 4 элементов геометрической прогрессии, необходимо вспомнить формулу для суммы n элементов геометрической прогрессии: Sn = a * (1 - r^n) / (1 - r), где Sn - сумма n элементов геометрической прогрессии, a - первый элемент прогрессии, r - знаменатель прогрессии, n - количество элементов прогрессии.

В нашем случае первый элемент a = 1 и знаменатель r = 3, так как каждый следующий элемент прогрессии получается умножением предыдущего элемента на 3. Нам нужно найти сумму 4 элементов, поэтому n = 4.

Подставляем все значения в формулу:
S4 = 1 * (1 - 3^4) / (1 - 3).
Упрощаем выражение:

S4 = 1 * (1 - 81) / (1 - 3).

Вычисляем (1 - 81) = -80 и (1 - 3) = -2.

S4 = 1 * (-80) / (-2).

Делим -80 на -2:

S4 = 40.

Сумма первых четырех элементов геометрической прогрессии 1, 3, 9 ... равна 40.