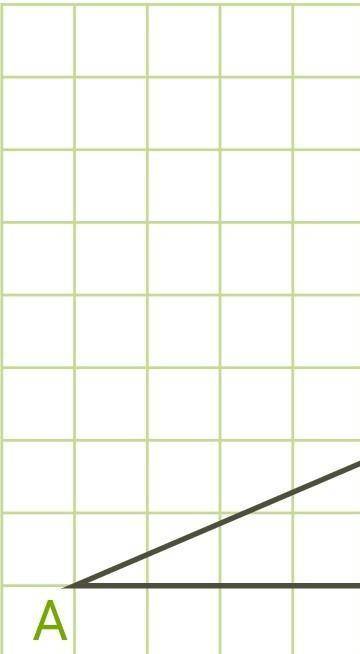
Найди синус угла, изображённого на рисунке, и умножь его на 58−−√. В ответе запиши только число. ​

Для решения данной задачи, нам понадобится найти значение синуса угла, изображённого на рисунке, и умножить его на число 58−−√.

Шаг 1: Найдем значение синуса угла, используя пропорцию согласно треугольнику на рисунке. В треугольнике дано, что противолежащий катет равен 12, а гипотенуза равна 20. Так как синус угла выражается соотношением sin(угол) = противолежащий катет/гипотенузу, то можем записать sin(угол) = 12/20.

Шаг 2: Упростим дробь 12/20. Найдём общий делитель для чисел 12 и 20, который равен 4. Разделим числитель и знаменатель на 4 и получим sin(угол) = 3/5.

Шаг 3: Умножим значение синуса угла на число 58−−√. Чтобы это сделать, мы умножаем числитель и знаменатель на 58−−√ и получаем (3*58−−√)/(5*58−−√).

Шаг 4: Упростим полученное выражение (3*58−−√)/(5*58−−√). Умножим числитель и знаменатель на (58+−−√) (противоположное значение 58−−√), что приведет к отмене значения под корнем и получим (3*58+−√)/(5*58+−√).

Шаг 5: Умножим числитель и знаменатель на 58+−√ (противоположное значение 58−−√), что также приведет к отмене значения под корнем, и получим (3*58+−√*58+−√)/(5*58+−√*58+−√).

Шаг 6: Упростим числители и знаменатели, умножив значения внутри скобок и получим (174+−√)/(290+−√).

Ответ: Значение синуса угла, изображенного на рисунке, и умноженное на 58−−√ равно (174+−√)/(290+−√).