Найди промежутки убывания функции
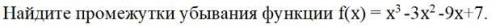
Другие вопросы по теме Математика
Популярные вопросы
- Сочинение по с примерами на тему время взросления...
2 - Нужно для 3 класса : in the playroom 1.complete the sentences with is or are 1)...
2 - Витя решил маме на день рождения подарить цветы если бы он купил 3 то у него осталось...
3 - Еки 10 алмурт болды.биреуи 1 алмурт, екиншиси 3 алмурт жегенде, олардын калган алмурттарынын...
2 - За 3 дня дети решили 17 во второй день решили на 2 меньше чем в 1 а в 3 на 3 меньше...
3 - Известно, что sin t + cos t = 0,2. найдите sin³t + cos³t....
1 - Вглавных подгруппах пс с увеличением заряда ядра радиус атомов как правило а) увеличивается;...
1 - 5прилогательных и 5 существительных с переводом...
3 - Выразите объёмы тел 4см3, 5 л, 7 мм3 в единицах си...
2 - Высота прямоугольного параллелепипеда 8см,стороны основания 5 и 6см. через меньшую...
3
Пошаговое объяснение:
f(x) = x³-3x²-9x+7
условие существования критических точек f'(x₀)=0
условие возрастания убывания функции:
если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
итак, ищем первую производную
f'(x) = (x³)'-3(x²)'-9(x)'+(7) = 3x²- 6x - 9
ищем критические точки
3x²- 6x - 9 = 0, отсюда х₁ = -1, х₂ = 3
получили промежутки (-∞ ;-1) (-1; 3) (3; +∞) на каждом отрезке возьмем значение производной, в точке, близкой к критической и принадлежащей отрезку
(-∞ ;-1)
например точка х = -2
f'(-2) = 15 >0 - функция возрастает
(-1; 3)
например точка х=0
f'(0) = -9 <0 - функция убывает
(3; +∞)
например точка х=4
f'(4) = 15 >0 - функция возрастает
ответ
промежуток убывания (-1; 3)