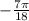Найди наибольший отрицательный корень уравнения sin 3x=1/2
Другие вопросы по теме Математика
Популярные вопросы
- Вмагазине было 12840 кг сахара до обеда продали 1905 кг сахара после обеда...
1 - Решить : мальчик предложил другу задумать число прибавить к нему 2 полученную...
1 - Подсчитайте какую кинетическую энергию имеет тело массой 1 кг при встрече...
3 - Сочинить мини сочинение на тему: вредные и съедобные грибы...
1 - Составь и реши по каждой строке таблицы.составь и реши обратные . 1 катер...
1 - Нужно описать/придумать конфликт из своей жизни и как вышла из этого конфликта...
1 - На двух полках 38 книг .сколько книг на каждой полке ,если на первой на...
1 - Выполни действия 7 м 2 дм - 42 дм 3 см...
2 - Какие страны имеют низкую ресурсообеспеченность и как они с этим справляются?...
3 - Минимум 5 предложений доказательства непри генералов к жизни повесть о...
1
Найдем первые отрицательные корни каждой серии решений:
1)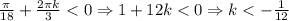
Т.к. k∈Z, то берем k = -1 ⇒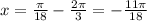
2)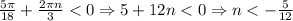
Т.к. n∈Z, то берем n = -1 ⇒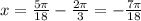
Из полученных отрицательных корней выберем наибольший: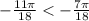
ответ: