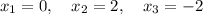Найди корни уравнения: 1) х^2-|х|=0 2) 2|х|-|х|^2=0 напишите с подробным решением.
Другие вопросы по теме Математика
Популярные вопросы
- Який об єм водню потрібен для відновлення 3 моль міді оксиду купррму...
2 - Муссонные дожди НЕ вызывают половодий на реках Янцзы и хуанхэхуанхэ...
3 - 34. Калейдоскоп заданий 1. Сопоставьте дату и событие.1928 годAПринятие...
2 - C2H6+O2→m(O2)=128г знайти V(CO2)=? н.у...
3 - Яка маса солі утвориться якщо 56г ферум (3) оксиду насипати до розчину...
1 - ТЕКСТ ЗАДАНИЯ Определите утверждение «верно», «неверно».Греческий...
1 - 5. Какое оптическое оборудование правильно описано? А) Телескоп...
3 - Көрермендердің театрға деген көзқарастары неліктен өзгерді деп ойлайсыңдар?...
3 - Запишите отношения между следующими значениями по формуле. Найдите...
3 - Начертите окружность радиуса 4 см с центром o проведен луч сначала...
1
1) Рассмотрим 2 случая
а)
тогда уравнение принимает вид
Оба корня удовлетворяют условию 1.
б)
тогда уравнение принимает вид
Последний корень не удовлетворяет 2-му условию. Значит он не является ответом.
ответ: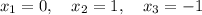
2) Снова рассматриваем 2 случая
тогда уравнение принимает вид
Оба корня удовлетворяют 1-му условию
б)
тогда уравнение принимает вид
Последний корень не удовлетворяет 2-му условию. Значит он не является ответом.
ответ: