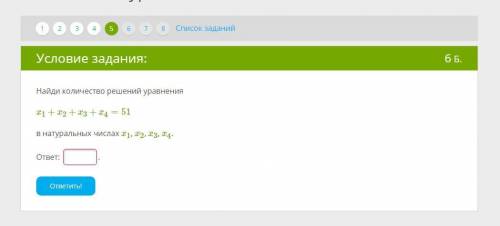
Найди количество решений уравнения x1+x2+x3+x4=51

в натуральных числах x1, x2, x3, x4.

ответ:19600

Пошаговое объяснение:

Представим число 51 суммой из 51 единички:

1+1+…+1=51.

Данная сумма содержит ровно 50 знаков +. Выберем в этой сумме три знака +, заменим перегородкой и найдём сумму единичек, ограниченных перегородками. Тем самым мы получим 4 натуральных числа, дающие в сумме 51.

Таким образом, мы построили взаимно однозначное соответствие между решениями нашего уравнения и выбрать три знака + из 50. Поскольку последнее можно осуществить

Получаем, что существует ровно 19600 решений у исходного уравнения.