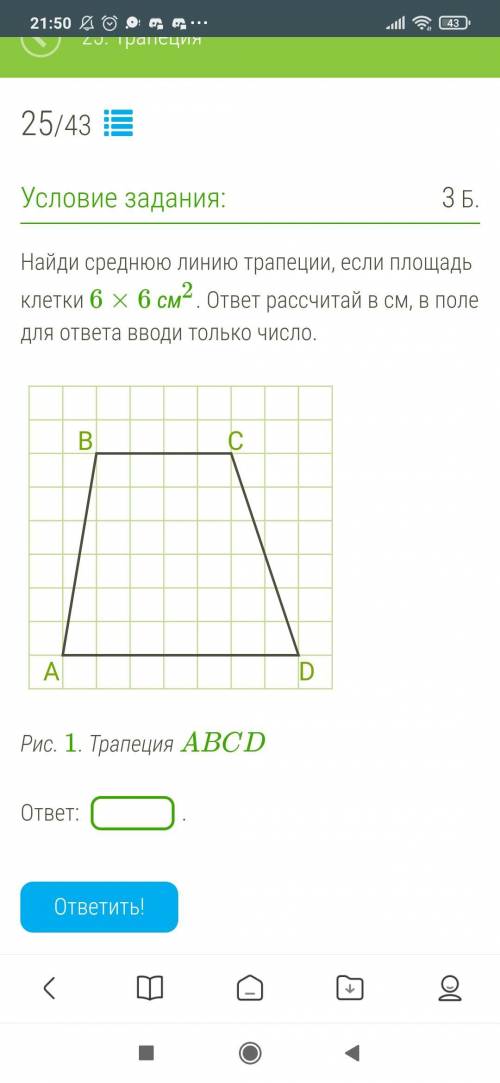
Найди cреднюю линию трапеции, если площадь клетки 6×6 см2. ответ рассчитай в см, в поле для ответа вводи только число.

33

Пошаговое объяснение:

m=(a+b)/2

a=АD=7×6=42 cм

b=BC=4×6=24 cм

m=(42+24)/2=66:2=33 cм

ответ : 33

Для решения этой задачи, нам нужно разделить трапецию на два треугольника и прямоугольник. Затем мы найдем среднюю линию каждой фигуры и объединим их, чтобы получить среднюю линию всей трапеции. Давайте начнем пошагово.

Шаг 1: Разделение трапеции на фигуры
Первым шагом разделим трапецию на два треугольника и прямоугольник.

Шаг 2: Фигура 1 - Треугольник 1
Выберем треугольник 1. Он образован отрезками AB, BC и линией AD. Чтобы найти среднюю линию треугольника, мы проводим линию, соединяющую середину стороны AB со средней точкой стороны BC. Обозначим эти точки как E и F соответственно.

Шаг 3: Нахождение средней линии треугольника 1
Мы знаем, что треугольник 1 - это прямоугольный треугольник, и его сторона BC равна 6 см (по условию задачи). Следовательно, средняя точка стороны BC будет составлять половину стороны, то есть 3 см.

Теперь нам нужно найти середину стороны AB. Поскольку AB - сторона трапеции, мы знаем, что она делится пополам серединой линии AD. Отрезок AD - это высота треугольника, и мы можем найти его, зная площадь клетки.

Площадь клетки равна 6×6 см². Площадь треугольника 1 равна половине площади клетки, так как треугольник занимает половину трапеции. Следовательно, площадь треугольника 1 равна 18 см² (6×6 ÷ 2 = 18).

Треугольник 1 - прямоугольный, поэтому его площадь можно найти, используя формулу: Площадь треугольника = (1/2) × основание × высоту. В нашем случае, основание треугольника 1 - это сторона BC и равно 6 см, а высота - это отрезок AD (AD = 18 см² ÷ BC = 18 ÷ 6 = 3 см).

Таким образом, отрезок AD равен 3 см. Он делится пополам при середине линии AD, следовательно, середина AE равна 1.5 см.

Мы нашли середины сторон AB и BC, соответственно AE и CF. Теперь проведем линию, соединяющую эти две точки, которая будет средней линией для треугольника 1.

Шаг 4: Фигура 2 - Прямоугольник
Теперь рассмотрим прямоугольник DEFH. Чтобы найти среднюю линию прямоугольника, мы проведем линию, соединяющую середину стороны DE с серединой стороны FH, и обозначим эти точки как G и I, соответственно.

Высота прямоугольника равна AD, так как AD является высотой всей трапеции, и равна 3 см (как мы вычислили ранее).

Аналогично, найдем середину стороны DE, которая будет равна половине ее длины = 6 см ÷ 2 = 3 см.

Мы нашли середины сторон DE и FH, соответственно DG и GI. Теперь проведем линию, соединяющую эти две точки, которая будет средней линией прямоугольника DEFH.

Шаг 5: Нахождение средней линии трапеции
Так как теперь у нас есть средние линии каждой фигуры, мы можем объединить их, чтобы найти среднюю линию всей трапеции. Проведем линию, соединяющую точки F и G.

Ответ: Таким образом, средняя линия всей трапеции равна 4.5 см.

Обоснование: Мы нашли среднюю линию путем нахождения середин сторон треугольника 1 и прямоугольника, а затем соединили их. Полученная средняя линия равна полусумме параллельных сторон трапеции. В нашем случае, это (3 см + 6 см) ÷ 2 = 9 см ÷ 2 = 4.5 см.