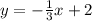Напишите уравнения прямых, проходящих через точку M ,
одна из которых параллельна, а другая – перпендикулярна заданной
прямой
l .
M (3; 1), l:3x-y+2=0.
Другие вопросы по теме Математика
Популярные вопросы
- 4. От имени главного героя рассказа приключения Тома Сойера глава два расскажите,...
1 - Установи соответствие между процессом и степенью окисления образовавшейся частицы:...
1 - Напишите к предложениям их времена. Aly family and I have taken part in a 10 mile...
2 - Какими политическими и культурными ограничениями столкнулись депортированные жители...
2 - Косвенная речь. Английский...
3 - Прочитай текст. Выпиши все местоимения, укажи их разряд. Какие части ре-Чи они замещают?...
2 - №1 Составьте формулы следующих веществ: оксид хлора (V), гидроксид бария, азотистая...
2 - Кто был погребен в Филипповском кургане...
1 - Распределите углеводороды по трем гомологическим рядам: алканы, алкены, алкины:...
3 - - Назвіть райони поширення льодовиків. Як ви думаєте, чому льодовики поширені на...
3
Перепишу немного уравнение прямой:
у=3х+2
Тогда все параллельные ей будут вида у=3х+а, найдем а:
Так как прямая должна проходить через точку М(3;1), заменим координаты в уравнении:
1=3*3+а
1=9+а
а=1-9
а=-8
Тогда уравнение параллельной прямой такое у=3х-8
Прямая перпендикулярная будет иметь такое уравнение: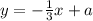
Заменим координаты в уравнении:
1=-1+а
а=1+1
а=2
Тогда уравнение перпендикулярной прямой такое