1. Математика
  2. Написать уравнения касательной

Написать уравнения касательной и нормали к заданной в неявном виде кривой F(x;y) = 0, проходящих через точку (x;y), координаты которой удовлетворяют условию: log
(x=15)
​


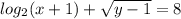
log_{2}(x + 1) + \sqrt{y - 1} = 8

ElizabetSnow ElizabetSnow    3   08.11.2020 22:15    16

Ответы
фиаско123 фиаско123  08.12.2020 22:16

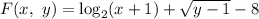Пусть F(x, ~ y) = \log_{2}(x+1) + \sqrt{y-1}-8 и задана в неявном виде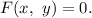 F(x, ~ y) = 0.

Тогда если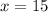 x = 15, то

\log_{2}(15+1) + \sqrt{y-1} - 8 = 0;

\log_{2}16 + \sqrt{y-1} - 8 = 0;

4 + \sqrt{y-1} - 8 = 0;

\sqrt{y-1} = 4;

y - 1 = 16;

y = 17.

Следовательно,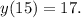 y(15)=17.

Найдем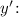 y' \colon

y' = \dfrac{dy}{dx} = \dfrac{-\dfrac{\partial F}{\partial x} }{\dfrac{\partial F}{dy} } = -\dfrac{F'_{x}}{F'_{y}} = -\dfrac{2\sqrt{y-1}}{\ln 2 (x+1)}

y'(15) = -\dfrac{2\sqrt{17-1}}{\ln 2 \cdot (15+1)} =\dfrac{2\sqrt{16}}{\ln 2 \cdot 16} = \dfrac{1}{2\ln 2}

Находим уравнение касательной:

y = y'(x_{0})(x - x_{0}) + y(x_{0})=\dfrac{1}{2\ln 2}(x - 15) + 17 = \dfrac{x - 15}{2\ln 2} +17

и уравнение нормали в этой же точке:

y = -\dfrac{1}{y'(x_{0})} (x - x_{0}) + y(x_{0})=-2\ln 2(x - 15) + 17

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Польди Польди  01.08.2019 20:20
В7 комнатах сидят 19 зайцев. может ли хотя бы в одной клетке быть нечетное число зайцев...
sushenkop08wf4 sushenkop08wf4  01.08.2019 20:20
Біля школи ростуть каштани і тополі каштанів росте 7 а тополь у 3 рази більше скільки дерев росте біля школи?...
lada48 lada48  01.08.2019 20:20
Фермерском хозяйстве 2 5 всего поля засеяли пшеницей 18 пользователей овощами площадь поля кризис фильмы с венецией на 17 гектаров больше площади площади поля, овощами...
serob1223 serob1223  01.08.2019 20:20
84 минус 48 разделить на 4 умножить на плюс 3 куда надо ставить скобки чтобы получилось 24...
mboyko2005 mboyko2005  01.08.2019 20:20
Выразить в см 5кл; 9дм 6см; 5дм1см; 11дм 3см...
cherkashina711 cherkashina711  01.08.2019 20:20
Емкость банки 3 л. количество 8 и 12 штук . емкость всех банок одинаковая . найти емкость второй банки....
Настенька192002 Настенька192002  01.08.2019 20:20
Упети 5 ручек, а у вики 3. сколько всего ручек?...
Mondy228 Mondy228  01.08.2019 20:20
На одной ферме 847 коров,а на другой-на 309 коров больше. сколько коров на двух фермах?...
timadva timadva  01.08.2019 20:20
6,7*(7,9-y)=28,81 9,14 х-(3,78 х+2,87 х)=12,45 (6,9-5,52: 0,63*0,85*((5-0,1+25): (3,7+0,05)...
кира671 кира671  01.08.2019 20:20
Как решить неравенство 4+12х 7+13х...

Популярные вопросы