1. Математика
  2. Написать уравнение окружности,

Написать уравнение окружности, проходящей через точки А(0 ; 3) и В(8 ; -5), если известно, что центр окружности лежит на прямой 2х+5у-10=0.

MeowthCopyright MeowthCopyright    2   05.08.2020 12:00    0

Ответы
SofiaAM SofiaAM  15.10.2020 15:42

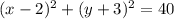
ответ:(x-2)^2+(y+3)^2=40

Пошаговое объяснение:

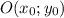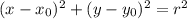
Уравнение окружности с центром в точке O(x_0; y_0) и радиусом r имеет вид: (x-x_0)^2+(y-y_0)^2=r^2

Про координаты центра известно, что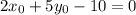 2x_0+5y_0-10=0, откуда получим, что 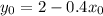y_0=2-0.4x_0 (1)

Еще мы знаем, что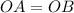 OA=OB, то есть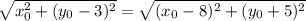 \sqrt{x_0^2+(y_0-3)^2}=\sqrt{(x_0-8)^2+(y_0+5)^2}

x_0^2+y_0^2-6y_0+9=x_0^2-16x_0+64+y_0^2+10y_0+25

16y_0=16x_0-80

y_0=x_0-5 (2)

Объединяя (1) и (2):

2-0.4x_0=x_0-5\\1.4x_0=7\\x_0=2

y_0=2-5=-3

r=OA=\sqrt{2^2+(-3-3)^2}=\sqrt{40}

Значит, уравнение окружности имеет вид:

(x-2)^2+(y+3)^2=40

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ЖекаБРО16 ЖекаБРО16  20.01.2021 10:43
Зведи дроби до спiльного знаменника.. ½ i 5/20 2) 4/15 i 3/10.3)9/32 i 1/64)¼ i ⅝.Cрочно ​...
stasvikulyа stasvikulyа  20.01.2021 10:43
2 Есепті шығар.дығыАрақашықтығы 54 км болатын екі айлақтан бір уақытта жәнебір бағытта қайық пен катер жолға шықты. Катердің жылдам-25 км/сағ, ал қайықтың жылдамдығы –...
Map21 Map21  20.01.2021 10:43
Көгалдандыру үшін екі көше бойына ағаштар отырғызылды. Бірінші көшедегі ағаштар саны екінші көшедегі ағаштар саны:нан 1,4 есе көп. 13 ағашты бірінші көшеден екінші көшеге...
Hydini Hydini  20.01.2021 10:43
Из 8кг винограда получается 2кг изюма. сколько процентов изюма содержится в 7кг винограда Составьте условие и пропорцию​...
kseniarevda7 kseniarevda7  20.01.2021 10:43
За 5 часов на мельнице смололи 45т муки. колько тонн можно смолоть за 7 часов?​...
ketrinkryt ketrinkryt  20.01.2021 10:43
Яка точка розміщена праворуч від іншоі 1)А(-4)чиВ(-8);2)С(6)чи(6.1);3)F(-0.001);4)G(-34/13)чиН(-3 3/11...
VikaSh86 VikaSh86  20.01.2021 10:44
и лучшии ответ памагите 3,4,5 ​...
veronikasimonova1 veronikasimonova1  20.01.2021 10:44
Даны векторы a = (4; 2; −1), b = (7; 9; 6), c = (3; 1; 3), d = (−10; 8; 3) в некотором базисе. Показать, что векторы a, b, c образуют базис и найти координаты вектора d...
kozltanya2013 kozltanya2013  20.01.2021 10:44
Накресліть кординатну пряму, взявши за одиничний відрізок чотири клітинки зошита, і позначте на ній точки. M(-2);K(1);P(0,5);D(-1/4);F(1,1/2)75);N(2 3/4);S(1 1/2)...
дэфолт123 дэфолт123  20.01.2021 10:45
1) |х|+3=5; 2) |у|-2=1; 3) |2х|+3=9; 4)|5у|-4=6; 5)3/7+|4х|=1; 6) 4+|3у|=7 Номер 824 только...

Популярные вопросы