Написать уравнение касательной к нормали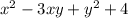
в точке пересечения с прямой y=x
с подробным решением

y=-0,5x+1;

Пошаговое объяснение:

уравнение нормали к функции в точке (x0;y0) имеет вид:

y-y0=-(x-x0)/y'(x0;y0)

Найдём точку пересечения кривой x²-3xy+y²+4=0 и прямой y=x.

Поставим значение y=x в уравнение кривой.

x²-3xx+x²+4=0;

x²-3x²+x²+4=0;

-x²+4=0;

x0=2.

y0=2.

То есть координаты точки пересечения (2;2)

Теперь найдём производную исходной кривой. Для этого дифференцируем её неявно:

(x²-3xy+y²+4)'=0;

2x-3y-3xy'+2y'=0;

2x-3y+y'(2-3x)=0;

y'(2-3x)=3y-2x;

y'=(3y-2x)/(2-3x);

подставляем координаты точки пересечения и находим значение производной в этой точке:

y'(x0;y0)=(3*2-2*2)/(2-3*2);

y'(x0;y0)=4/(-4);

y'(x0;y0)=-1;

Теперь подставляем найденные значения в уравнение нормали:

y-2=-(x-2)/-1;

y=-0,5x+1;

Вроде так как-то