Написать уравнение касательной к графику у=1/(1+х^2) в точке с абсциссой х0=1
Ответы
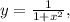
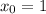
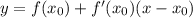 - уравнение касательной
- уравнение касательной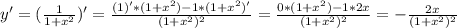
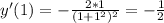
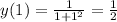
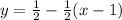
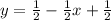
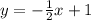 - уравнение касательной
- уравнение касательной
Другие вопросы по теме Математика
Популярные вопросы
- Определите значение переменной а после выполнения фрагмента программы:...
2 - История древней литературы...
2 - решить задачу:Мама купила для сына джинсы, футболку и носки. Джинсы стоят...
3 - Заполните таблицу власть Юнлэ и Токугава. Аргументы и доказательства очень...
2 - А. А. А.. А. А. А. А. А. А. А. А. А. ...
3 - Внимательно ознакомьтесь с материалом урока. Выполните кроссворд в тетради...
2 - Изобрази на графике №1 x ≤ 3 №2 3≤x≤8 и -2≤y≤1 №3 y={x во 2 степени при...
3 - як хартія вольностей захишала різні версти Англійського населеня...
3 - Естес ртс 2 часть 13-144 класс скиньте...
2 - Знайдіть:|–15,4| (Введіть значення)...
1