Написать полный дифференциал функции
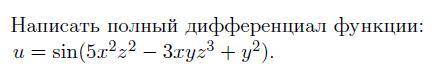
Другие вопросы по теме Математика
Популярные вопросы
- Составьте памятку о бережном отношении к пресной воде для Жителей Алматы....
3 - 4. В вакууме два точечных заряда 3 нКл и 9 нКл отталкиваются друг от друга...
2 - Обчисли кількість речовини яка містить у 8 г карбонату (Са СD3) вычисли количество...
2 - В 270 г раствора, насыщенного при 50 °С содержится 120 г нитрата свинца....
2 - ,геометрия 8 клас 2 тоқсан бойынша жиынтык багалау...
1 - , ответьте на любые 5 вопросов...
1 - Изобразите все силы графических в масштабе 1 клетка равна 2 Н...
3 - ,сегодня контрольная 1. определить плотность вещества массой 250 г, объем...
2 - В треугольнике BKN угол K =80 градусам угол B= 60 градусам AC=4 √2...
1 - нужно написать не только ответ ,но и решение...
3
Пошаговое объяснение:
Вспомним формулу полного дифференциала функции
Находим частные производные
Дополняем формулу