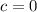Написать формулу лагранжа для функции f(x)=x^(4/3) и найти с на [-1; 1]
Другие вопросы по теме Математика
Популярные вопросы
- Сообщение на тему ,, сезонные изменения птиц нашего региона Крыма 10 15 предложений...
2 - Решите Номер 85a,87а,88а....
3 - 841. Учитывая, что вещества состоят из молекул, между котора ми есть промежутки,...
3 - Бліц-обговорення Чому саме такі умови було сформульовано в цьому документі? Що в...
2 - Choose the correct words. (10 marks) 1 Did I yet / already / ever tell you about...
1 - Пусть ABCA1B1C1 — прямая призма, в основании которой лежит равнобедренный прямоугольный...
3 - вершина а трикутника авс належить площині &, а вершина вс їй не належить. пряма...
1 - К какой группе относятся профессионализмы и диалектизмы...
3 - Почему важно знать устаревшую лексику русского языка...
2 - Как ваши дела? в школе как? устали? споки^^...
3
c=0
Пошаговое объяснение:
Запишем формулу Лагранжа в общем виде
Вычислим производную функции
Тогда:
Откуда