Наглядная геометрия 8 класс
решить 73 задание
Другие вопросы по теме Математика
Популярные вопросы
- Пришвин и утята как автор относятся к поступку...
3 - Паскаль! дан одномерный массив целых чисел (n=15).вставить число k перед последним...
1 - Написать маленький текст про одуванчик...
2 - Вволейбол играют 30 детей, из которых 30% девочек, сколько мальчиков играют в...
1 - На аэродроме было 42 самолетов и 6 вертолетов. несколько машин поднялись в воздух....
3 - С-0.8с-1/4с-1/2с ж) 0.3а-0.2в-0.7а+0.2в з)4а-6а2а+12-11 и)2/3а+3/8b-1/6а-1/4b...
3 - Сколкоь разных многуголников на каждом чертеже назови их....
3 - 4. самостоятельная деятельность граждан по решению вопросов местного значения...
1 - Всаду 20 деревьев, из них 4\5 вишни. сколько вишен в саду?...
2 - Поставь скобки так чтобы равенства стали верными 15*40-40: 4: 2=225...
1
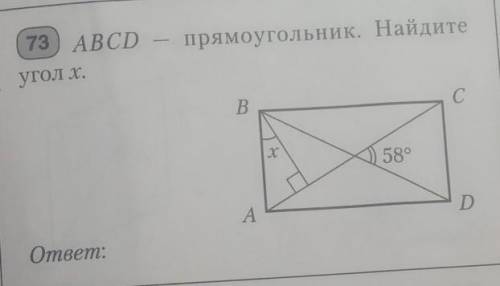
Пусть т. O - центр пересечения диагоналей прямоугольника ABCD.
Тогда углы AOB и DOB - равны, как вертикальные.
Рассмотрим треугольник AOB:
Со свойства прямоугольника - диагонали равны и точкой пересечения делятся пополам, то есть BO = AO. С определения треугольник AOB - равнобедренный.
С теоремы о сумме углов треугольника:
180° = ∠OAB + ∠ABO + ∠AOB
Со свойства равнобедренного треугольника:
∠OAB = ∠ABO, тогда:
180° = ∠ABO + ∠ABO + 58°
2 · ∠ABO = 180° - 58°
2 · ∠ABO = 122°
∠ABO = 61° = ∠OAB
Рассмотрим треугольник ABH (Прямая BH, перпендикулярна AC)
Со свойства о сумме углов треугольника:
∠HAB + ∠x + ∠BHA = 180°
∠HAB = ∠OAB, тогда:
61° + ∠x + 90° = 180°
∠x = 29°
ответ: 29 градусов.