Наглядная геометрия 5 класс стр 53-54 номера 9,10,11

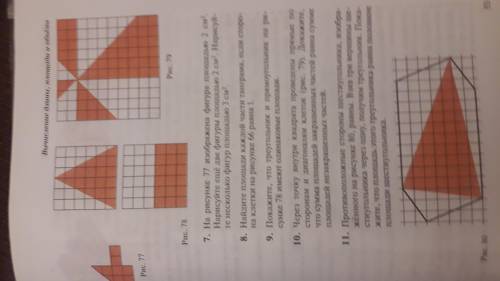
номер 9

площадь прямоугольника на р сунке 78 равна 3 кл. умножить на 6 кл. = 18 кл.

площадь треугольника равна 18 (посчитать квадраты на рисунке)

Давай начнём с решения задачи номер 9.

В задаче нам дано, что $AB = BC$ и $CD = CE$. Мы должны найти, верно ли, что $AC = DE$.

Мы можем доказать или опровергнуть это, применив свойство равных сторон треугольника. Если два треугольника имеют две равные стороны и равные углы между ними, то они равны как по стороне, так и по углам.

Давайте рассмотрим треугольники $ABC$ и $CDE$. Они имеют две равные стороны: $AB = BC$ и $CD = CE$, и у них есть общий угол $\angle BCD$ (угол при вершине $C$).

Таким образом, мы можем сделать вывод, что треугольники $ABC$ и $CDE$ равны по стороне и углам. Используя это свойство равных треугольников, мы можем сказать, что $AC = DE$. Ответ на задачу номер 9 - "Да, верно что $AC = DE$".

Теперь перейдём к решению задачи номер 10.

В задаче нам дано, что $AD = DB$ и $BE = EC$. Мы должны найти, верно ли, что $AC = DE$.

Аналогично задаче номер 9, мы можем применить свойство равных сторон треугольника, чтобы доказать или опровергнуть это.

Рассмотрим треугольники $ADB$ и $BEC$. Они имеют две равные стороны: $AD = DB$ и $BE = EC$, и общий угол $\angle B$.

Однако, в отличие от задачи номер 9, у нас нет информации о равенстве углов между этими сторонами. Мы не знаем, равны ли углы $\angle BAD$ и $\angle CBE$.

Поэтому, мы не можем сделать вывод о равенстве треугольников $ADB$ и $BEC$. Мы не можем утверждать, что $AC = DE$. Ответ на задачу номер 10 - "Нет, не верно, что $AC = DE$".

Наконец, перейдём к решению задачи номер 11.

В задаче нам дано, что $AM = MB$ и $CN = NE$. Мы должны найти, верно ли, что $AC = DE$.

Опять же, мы можем использовать свойство равных сторон треугольника для доказательства или опровержения этого.

Рассмотрим треугольники $AMC$ и $BNE$. Они имеют две равные стороны: $AM = MB$ и $CN = NE$, и общий угол $\angle MNC$.

Так как у нас есть информация о равенстве одного угла между этими треугольниками, мы можем сделать вывод, что треугольники $AMC$ и $BNE$ равны по стороне и углам. Тогда $AC = DE$. Ответ на задачу номер 11 - "Да, верно, что $AC = DE$".

Таким образом, мы решили все три задачи, используя свойство равных сторон и углов треугольника.