надо
у-1 /2- 2у+3 /8- у>2
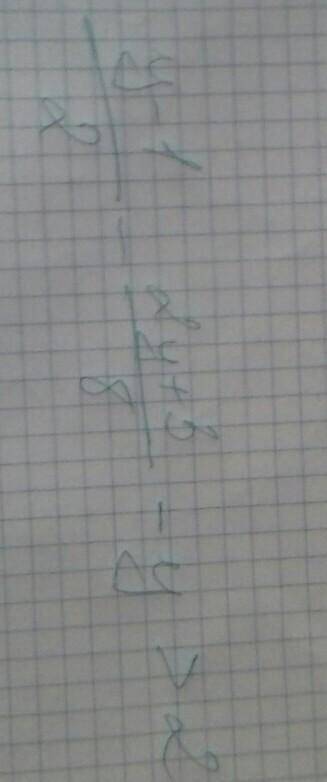
Другие вопросы по теме Математика
Популярные вопросы
- One word in each sentence is wrong. Underline it. Write the correct word...
1 - решить похідну(7-5x+6x⁴-x¯5+2x¯10-x) ...
2 - Что общего стихотварения с былиной...
3 - 27000:(х-15)=19 шығарып беріндерш...
1 - Ә) Ертегі құрап жаз. Баяғы өткен заманда … болыпты. Ол үнемі үйінетасыпты....
2 - Составьте таблицу: «Реформы и реформаторы в России»...
3 - я вас пролайкаю и поставлю все...
2 - тексту составьте диалог қазақ халқының ақыны -Алматы облысының Нарынқол...
2 - Help me... Help me, Help me...
1 - Мяч брошен вертикально вверх. Время падения мяча в n раз больше времени...
1
5
у-1 /2- 2у+3 /8- у>2=у < 3
6
Нам дано неравенство: (у-1)/(2-2у) + (3)/(8-у) > 2
Шаг 1: Сокращение дроби слева от знака ">".
Для начала, нужно найти общий знаменатель для дробей слева от знака ">".
Общий знаменатель - произведение исходных знаменателей, в данном случае, это (2-2y)(8-y).
Для упрощения рассмотрим каждую дробь по отдельности.
Умножим первую дробь (у-1)/(2-2у) на (8-y)/(8-y):
((у-1)(8-y))/((2-2у)(8-y)) + (3)/(8-у) > 2
Шаг 2: Сокращение дроби справа от знака ">".
Вторая дробь уже имеет общий знаменатель с первой дробью, поэтому ее оставляем без изменений.
((у-1)(8-y))/((2-2у)(8-y)) + (3)/(8-у) > 2
Шаг 3: Сокращение дробей слева от знака ">".
Раскроем скобки и приведем дроби к общему знаменателю:
(8у-8-у²+y)/((2-2у)(8-y)) + (3)/(8-у) > 2
Шаг 4: Упрощение уравнения.
Теперь сложим дроби слева от знака ">":
(8у-8-у²+y+3(2-2y))/((2-2у)(8-y)) > 2
(8у-8-у²+y+6-6y)/((2-2у)(8-y)) > 2
(7 у-у²-5 у+8+6)/((2-2у)(8-y)) > 2
(-у²+2у+14)/((2-2y)(8-y)) > 2
Шаг 5: Приведение неравенства к удобной форме.
Перенесем все в левую сторону:
(-у²+2у+14)/((2-2y)(8-y)) - 2 > 0
Шаг 6: Приведение неравенства к общему знаменателю.
Умножим обе части неравенства на (2-2y)(8-y):
(-у²+2у+14) - 2(2-2y)(8-y) > 0
Шаг 7: Раскрытие скобок.
Упростим выражение в правой части неравенства:
-у²+2у+14 - 2(16-10y+2y²) > 0
-у²+2у+14 - (32-20y+4y²) > 0
-у²+2у+14 - 32+20у-4у² > 0
-5у²+22у-18 > 0
Шаг 8: Сокращение и упрощение уравнения.
Нам нужно решить это уравнение. Сначала упростим его:
5у²-22у+18 < 0
Шаг 9: Решение квадратного уравнения.
Теперь решим это квадратное уравнение. Мы можем найти корни уравнения, используя формулу дискриминанта:
D = b²-4ac
у = (-b±√(D))/(2a)
где a = 5, b = -22 и c = 18.
D = (-22)²-4(5)(18)
D = 484-360
D = 124
Так как D > 0, у нас есть два корня уравнения.
у = (-(-22)±√(124))/(2(5))
у = (22±√(124))/(10)
у = (22±2√(31))/(10)
у = (11±√(31))/(5)
Шаг 10: Проверка корней уравнения.
Теперь, чтобы найти, в каком интервале значения у удовлетворяют неравенству, выполним проверку с использованием тестовой точки в каждой области. Например, возьмем y = 0:
(-5(0)²+22(0)-18) < 0
-18 < 0
Значит, точка y = 0 удовлетворяет неравенству.
Теперь возьмем y = 3:
(-5(3)²+22(3)-18) < 0
-39 < 0
Значит, точка y = 3 удовлетворяет неравенству.
Таким образом, решением данного неравенства является у ∈ (11-√(31))/5, (11+√(31))/5.
Надеюсь, это помогло вам понять, как решить данную математическую задачу. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их.