надо! вычеслить определенный интеграл 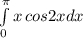
Другие вопросы по теме Математика
Популярные вопросы
- Какую формулу имеет вещество с полярной ковалентной связью?...
2 - Функция задана формулой y=-7x -1.найдите координаты точки пересечения графика...
3 - Как правильно решать уравнения со с кобками и без обясните...
3 - Кто создан из камня, кто создан из глины, - а я серебрюсь и сверкаю! мне...
3 - Выражение если можно то подробно b/a-b: (a/a-b-a+b/a)...
3 - Просклонять словосочетание: 2014 год(буквами )...
2 - решите уравнение: 4,3*(15x-2x)=11,18...
1 - Вопросы для викторины о греции и италии по окружающему миру 3 класс!...
1 - Два луча на рассеивающую линзу параллельно её главной оптической оси.покажите...
3 - Ширина прямоугольника 14,длина в 3 раза больше.найди площадь и периметр...
1
Найдем неопределённый интеграл, потом подставим пределы:
по частям:
С пределами: