Надо найти корни уравнения

х = π/3

Пошаговое объяснение:

Теория:
sin(2α) = 2sin(α)cos(α) - синус двойного угла

Решение:
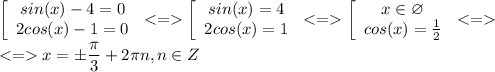
sin(2x)-8cos(x)-sin(x)+4 = 0;
2sin(x)cos(x)-sin(x)-8cos(x)+4 = 0;
sin(x)*(2cos(x)-1)-4*(2cos(x)-1) = 0;
(sin(x)-4)(2cos(x)-1) = 0;
Произведение равно нулю, когда один из множителей равен нулю

Очевидно, что в промежутке х∈(0;π/2) лежит одно значение х = π/3