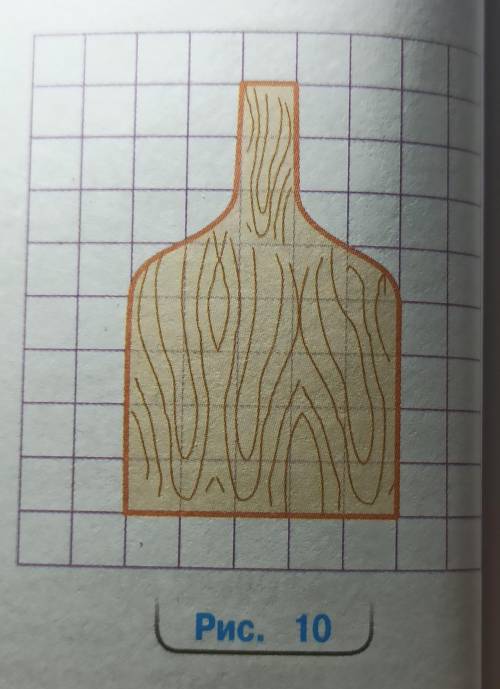
На уроке технологии мальчики выпиливали из фанеры разделочные доски. Сначала они с компьютера рисовали на сетке шаблон доски, например, такой, как показано на рисунке 10. а) Какую площадь имеет этот шаблон, если площадь ячейки составляет 1 ед.²? б) Какие наибольшие размеры в сантиметрах может иметь одна ячейка, чтобы разделочную доску можно было выпилить из фанеры прямоугольной формы длиной 50 см и шириной 24 см? в)Какую площадь будет иметь разделочная доска в натуральную величину, если размер клетки 6×6 см !

а) Для нахождения площади шаблона, нам нужно посчитать количество ячеек внутри шаблона и умножить его на площадь одной ячейки.
На данном шаблоне видно, что по ширине есть 10 ячеек, а по высоте - 6 ячеек. Значит общее количество ячеек равно 10 * 6 = 60 ячеек.
Площадь одной ячейки равна 1 ед.².
Тогда площадь шаблона будет равна 60 * 1 = 60 ед.².

б) Чтобы найти наибольшие размеры одной ячейки, чтобы разделочную доску можно было выпилить из фанеры, нужно проверить, какое наименьшее расстояние между соседними ячейками внутри шаблона.
Дано:
Длина фанеры - 50 см = 500 мм
Ширина фанеры - 24 см = 240 мм

Минимальное расстояние между соседними ячейками - это размер одной ячейки. Пусть он равен x см.
Тогда наименьшее количество ячеек по длине будет равно 500 / x, а по ширине - 240 / x.
Мы хотим найти максимальное значение x, при котором 500 / x и 240 / x являются целыми числами, иначе фанеру нельзя будет разделить на ячейки целым количеством.

Определим наибольший общий делитель для 500 и 240, который даст нам наибольшее значение x.
Общий делитель чисел 500 и 240 - это 20.
Значит, наибольшие размеры одной ячейки, чтобы разделочную доску можно было выпилить из фанеры, составят 20 см.

в) Чтобы найти площадь разделочной доски в натуральную величину, нужно учесть масштабирование пропорций. На шаблоне размеры ячейки составляют 1 ед.², а настоящая доска будет в масштабе 6×6 см.
Площадь одной ячейки в натуральной величине будет равна (6 см) * (6 см) = 36 см².

Мы знаем, что площадь шаблона равна 60 ед.².
Переведем ее в сантиметры:
60 ед.² * 36 см²/1 ед.² = 2160 см².

Ответ: Разделочная доска в натуральной величине будет иметь площадь 2160 см².