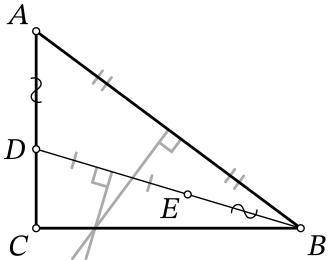
На стороне прямоугольного треугольника (угол — прямой) отмечена точка . На отрезке отмечена точка так, что =. Оказалось, что серединные перпендикуляры к отрезкам и пересекаются на отрезке . Найдите длину отрезка , если известно, что =10, =8
Другие вопросы по теме Математика
Популярные вопросы
- назвіть основні групи природних ресурсів океанів. які з них людина...
3 - Решить пропорцию 14x+1026= 1213...
1 - READ THE TEXT THEN DO TASKS. TASK 1. CHOOSE THE CORRECT ANSWER. ACCORDING...
3 - Задача по Физике на правила Кирхгофа...
3 - Сочинение- сравнительное описание Святогора и Ильи Муромца...
3 - 25 {xy}^{2} - 5 {y}^{2}25xy 2 −5y 216 {a}^{2} - 0.01 {c}^{2}16a 2...
2 - До зробити задачу У магазині 400 кг помідорів. До обіду продали 3/5...
3 - Розвяжіть рівняня 2×х 11...
3 - чем отличается герой рассказа мгновение Короленко от обычных людей?...
3 - Внесок українських учених у розвиток електрозварюваннянужен реферат...
1
Давайте обозначим точку пересечения серединных перпендикуляров как точку О.
1. Длина отрезка OM:
Дано, что длина отрезка AM равна 10, а длина отрезка BM равна 8. Так как точка М является серединой отрезка AB, то длина отрезка OM будет половиной суммы длин отрезков AM и BM:
OM = (10 + 8) / 2 = 18 / 2 = 9.
Таким образом, длина отрезка OM равна 9.
2. Длина отрезка OA:
Длина отрезка OA равна половине длины отрезка AM: OA = AM / 2 = 10 / 2 = 5.
Таким образом, длина отрезка OA равна 5.
3. Длина отрезка OB:
Длина отрезка OB равна половине длины отрезка BM: OB = BM / 2 = 8 / 2 = 4.
Таким образом, длина отрезка OB равна 4.
4. Длина отрезка AB:
Мы можем найти длину отрезка AB, используя теорему Пифагора для треугольника AOB.
Так как треугольник AOB прямоугольный, то применим теорему Пифагора:
AB^2 = OA^2 + OB^2
AB^2 = 5^2 + 4^2
AB^2 = 25 + 16
AB^2 = 41
Чтобы найти длину отрезка AB, возьмем квадратный корень от обеих сторон уравнения:
AB = √41
Таким образом, длина отрезка AB равна √41.
Итак, мы нашли длину всех отрезков в задаче:
- OM = 9,
- OA = 5,
- OB = 4,
- AB = √41.