На стороне ab трапеции авсd (bc||ad) взята точка к так, что ак: кв=2: 3. точка о - пересечение отрезков кс и bd, точка м - пресечение двух прямых: одна из них проходит через точки а и d, другая - через к и с. известно, что ad: bc=2: 1. найдите отношение площадей треугольников овс и осd.

Треугольники OBC и OCD имеют одинаковую высоту (основания BO и OD лежат на одной прямой и оба имеют общую вершину C), значит, их площади относятся как длины оснований: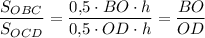

По теореме Менелая для треугольника ABD:

Треугольники AMK и BCK подобны по двум углам (∠AKM и ∠BKC вертикальные, ∠AMK и ∠KCB накрест лежащие):

ответ: 3:8