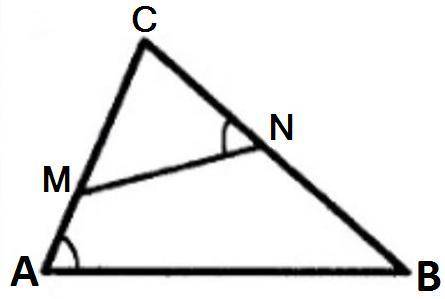
На рисунке угол А равен углу N найти подобные треугольники на рисунке и доказать их подобие

На данном рисунке изображены два треугольника - треугольник ABC и треугольник MNP. Нам нужно найти подобные треугольники на рисунке и доказать их подобие, учитывая, что угол А равен углу N.

Чтобы найти подобные треугольники, мы должны проверить, удовлетворяют ли они следующим двум условиям:

1. Углы в обоих треугольниках равны.
2. Стороны треугольников пропорциональны.

1. Углы в треугольниках:

На рисунке видно, что угол А равен углу N. Это значит, что один угол в обоих треугольниках равен. Остается проверить, равны ли остальные углы в треугольниках.

Если посмотреть на треугольник ABC, мы можем заметить, что угол C прямой (равен 90 градусов), а угол B - острый (меньше 90 градусов). Также, по условию, угол А равен углу N. Исходя из этого, можем предположить, что углы B и C в треугольнике MNP тоже будут острый и прямой, но это только предположение.

2. Стороны треугольников:

Чтобы проверить пропорциональность сторон треугольников, мы должны рассмотреть соотношение между длинами сторон в треугольнике ABC и треугольнике MNP.

Сначала определим соотношение сторон треугольника ABC. Заметим, что сторона AB противолежит углу C, а сторона AC - углу B. Таким образом, мы можем сказать, что соотношение сторон треугольника ABC будет следующим: AB/AC.

После этого рассмотрим соотношение сторон треугольника MNP. Аналогично, сторона MN противолежит углу P, а сторона NP - углу M. Мы можем записать соотношение сторон треугольника MNP как MN/NP.

Если треугольники ABC и MNP подобны, то эти соотношения должны быть равны. То есть, AB/AC = MN/NP.

Теперь давайте продолжим и проверим пропорциональность сторон этих треугольников.

На рисунке не приведены значения длин сторон треугольников, но судя по длине отрезков на рисунке, мы можем предположить, что сторона AB больше стороны MN, а сторона AC больше стороны NP. То есть, AB > MN и AC > NP.

Таким образом, мы можем записать отношения сторон треугольников ABC и MNP следующим образом: AB/AC > MN/NP.

Из этого следует, что треугольники ABC и MNP не являются подобными, так как их стороны не пропорциональны.

Итак, мы не можем найти на рисунке подобные треугольники, так как условия для подобия треугольников не выполняются.