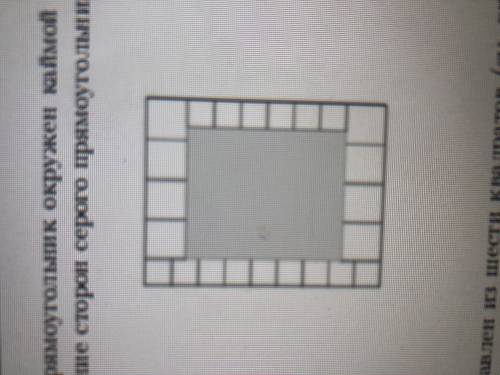
На рисунке серый прямоугольник окружен каймой двух разных размеров. Найдите отношение сторон серого прямоугольника

Пошаговое объяснение:

На левой стороне 9 маленьких кубиков, а на правой такое же расстояние занимают 6 маленьких и два больших. Следовательно 2Б = 3М.

Верхняя сторона серого прямоугольника равна 2*2Б-1M=6M-1M=5M

Правая сторона серого прямоугольника равна 6М

Отношение сторон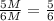

============            

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"      

Бодрого настроения и добра!    

Успехов в учебе!

Чтобы найти отношение сторон серого прямоугольника, мы должны сначала понять, как он связан с остальными фигурами на рисунке.

В данном случае, серый прямоугольник окружен двумя каймами разных размеров. Первая кайма состоит из двух прямоугольных фигур, а вторая - из четырех. Перейдем к решению шаг за шагом:

Шаг 1: Определение отношений сторон прямоугольников внутри каймы
Посмотрим на первую кайму, состоящую из двух прямоугольных фигур. Один прямоугольник внутри каймы имеет ширину, равную 18 см, и длину, равную 20 см. Другой прямоугольник имеет ширину, равную 12 см, и длину, равную 18 см. Мы можем использовать эти значения, чтобы найти отношение сторон прямоугольников внутри каймы.

Отношение ширины первого прямоугольника к длине:
18 см / 20 см = 0.9

Отношение ширины второго прямоугольника к длине:
12 см / 18 см = 0.67

Шаг 2: Определение отношений сторон каймы к серому прямоугольнику
Посмотрим на вторую кайму, состоящую из четырех прямоугольных фигур. Одна из прямоугольных фигур внутри второй каймы может быть рассмотрена как серый прямоугольник, так как он имеет те же стороны. Это значит, что отношение сторон второй каймы к серому прямоугольнику будет такое же, как и отношение сторон прямоугольников внутри первой каймы.

Отношение ширины второй каймы к длине серого прямоугольника:
0.9 (отношение первого прямоугольника внутри первой каймы) / 0.67 (отношение второго прямоугольника внутри первой каймы) ≈ 1.34

Ответ: Итак, отношение сторон серого прямоугольника составляет приблизительно 1.34 (ширина к длине).