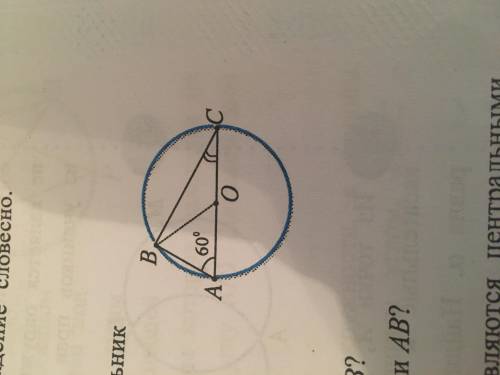
На рисунке представлен прямоугольный треугольник АВС- В=90 градусов, А=60 град, АС- диаметр. Проведите ОВ; допустим, ОВ=r. Найдите: а) Дуги АВ, ВС, АВС
Выразите АВ,ВС,АС через r. АС=2АВ. Каково соотношение между дугами АВС и АВ
Другие вопросы по теме Математика
Популярные вопросы
- Может ли человек проявиться как личность вне общества? Аргументируй свой...
1 - С момента изобретения радио понадобилось 40 лет, чтобы число слушателей в США...
2 - Каким образом современное общество влияет на социализацию индивида?...
3 - Почему людей волнуют вопросы о смысле жизни? Как сделать правильный выбор жизненных...
1 - Некоторые называют глобализацию не «всемирным братством», а «всемирным пиратством»....
2 - Какие изменения происходят в современном обществе?...
1 - Какие признаки человека характеризуют его как индивидуальность, а какие — как...
1 - Л. Н. Толстой писал: «В безнравственном обществе все изобретения, увеличивающие...
2 - Почему учёные характеризуют общество как форму совместной жизнедеятельности людей?...
1 - Как соотносятся понятия «человек» и «общество»?...
3
Пошаговое объяснение:
вопрос не очень поняла
что именно надо найти, но на рисунке написала все свойства
Пошаговое объяснение:
Дано:
прямоугольный треугольник АВС
∠ В=90°
∠А=60 °
АС- диаметр
Найти:
Дуги АВ, ВС, АВС
Вопрос 1:
Рассмотрим прямоугольный треугольник ΔABC :
В прямоугольном треугольнике ΔABC ,AC есть диаметр ⇒ AO=OC=R ,но так как BO есть тоже радиус,то AO=OC=BO=R.
BO образует с углом ∠BAO треугольник ΔABO и он равносторонний ,потому что
AO=BO=R - есть признак равнобедренности ,а тогда ∠ABO=∠BAO=60°,тогда угол ∠AOB можно найти ∠AOB = 2*(180°-(90°+60°)) = 60° ⇒ AB=BO=AO - треугольник ΔABO - равносторонний.
∠AOB в равностор. треугольнике ΔABO является центральным углом опирающийся на дугу AB. По свойству об опирающимся центральном угле на дугу , ∠AOB = ∪AB = 60°
BO c другой стороны образует ΔBOC - равнобедренный,т.к. BO=OC=R
∠BOC в ΔBOC есть центральный угол,который опирается на ∪ BC ⇒ ∠BOC=∪ BC = 180°-∠AOB = 180° - 60°= 120°
Дуга ∪ ABC есть сумма двух частей ∪ AB и ∪ BC :
∪ AB + ∪ BC = ∪ ABC = 180°
Первую часть вопроса понял ,а остальное нет