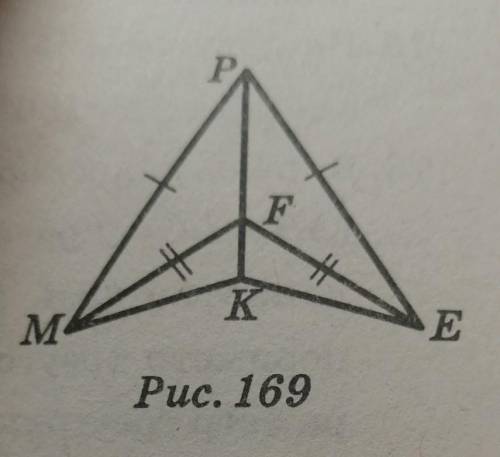
На рисунке MP=PE, MF=FE. Докажите, что теругольник MKP= EKP​

Для доказательства равенства треугольников MKP и EKP нужно показать, что их соответствующие стороны и углы равны. В данном задании у нас есть информация о длинах сторон треугольника MKP и EKP, а именно MP=PE и MF=FE. Шаг 1: Найдем углы МФе и МКр, используя данные о длине сторон. - Для этого построим высоты МH и EK, опущенные из вершин M и E соответственно. - Так как MP=PE и MF=FE, то высоты МH и EK будут равны, так как это высоты, опущенные из одной и той же стороны треугольника на равноудаленные точки. - Также, по теореме о прямых, перпендикулярных к одной и той же прямой, угол МФе равен углу МКр, так как они являются соответственными вертикальными углами. - Полученное мы можем сказать, что у этих треугольников есть две равные стороны и равные соответствующие углы. Шаг 2: Учитывая углы и стороны, можно заключить, что треугольники MKP и EKP равны. - Согласно теореме о равности треугольников, если у двух треугольников равны две стороны и равен соответствующий угол между ними, то треугольники равны. - У нас есть две равные стороны MP=PE и MF=FE, а также равные углы МФе и МКр. - Таким образом, мы можем заключить, что треугольник MKP равен треугольнику EKP. Таким образом, мы доказали, что треугольники MKP и EKP равны.