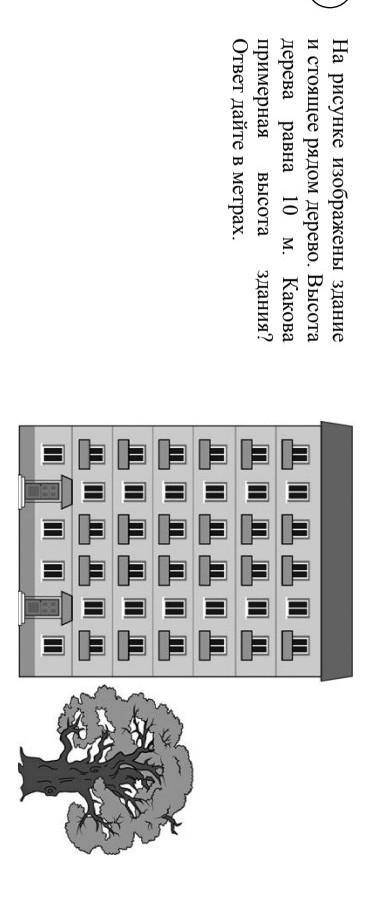
на рисунке изображены здание и стоящее рядом дерево высота дерева равна 10 м какова примерная высота здания​

Добрый день! Давайте решим эту задачу вместе.

На рисунке видно, что высота дерева равна 10 метрам. Нам нужно найти примерную высоту здания. Давайте посмотрим на рисунок и обратим внимание на то, что дерево и здание являются подобными объектами.

Что такое подобные объекты? Подобные объекты имеют одинаковые углы, но могут отличаться в размерах. В этой задаче мы знаем высоту дерева, но не знаем высоты здания.

Теперь нам нужно использовать сходство фигур для решения задачи. Мы можем использовать пропорции для этого. Пропорции помогут нам установить соотношение между высотой дерева и высотой здания.

Пусть х будет обозначать примерную высоту здания в метрах. Тогда мы можем записать пропорцию:

дерево/здание = высота дерева/высота здания.

Заменяя значения в пропорции, получаем:

10/х = 10/х.

Для решения пропорции мы можем использовать кросс-умножение. То есть, умножаем числитель первой дроби на знаменатель второй дроби и приравниваем его к умножению числителя второй дроби на знаменатель первой дроби:

10/х = 10/х.

Мы видим, что числитель и знаменатель равны, поэтому пропорция выполнена. Это означает, что примерная высота здания будет такой же, как высота дерева, то есть 10 метров.

Таким образом, примерная высота здания равна 10 метрам.

Я надеюсь, что мое объяснение было понятным и что я помог вам с решением этой задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать их.