На рисунке изображены две прямые, пересекающиеся в точке в. найдите координаты этой точки.

Чтобы решать, нужно привести уравнения к одному виду:

2х-у=6                                  х+2у=8

у= -2х+6                               у=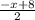

Чтобы найти точку пересечения прямых, нужно приравнять оба уравнения:

-2х+6 =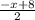

Чтобы решить пользуемся свойством пропорции:

2(-2х+6) = 1(8-х)

-4х+12 = 8-х

-3х = -4

х = 1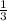 - это ордината точки

Теперь найдем абциссу, подставив в первоначально уравнение х:

2у = 8-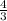

2у =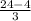

у =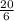

у =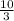

у = 3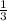

Итак, мы получили точку: (1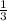;3)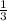

Удачи от Беллы