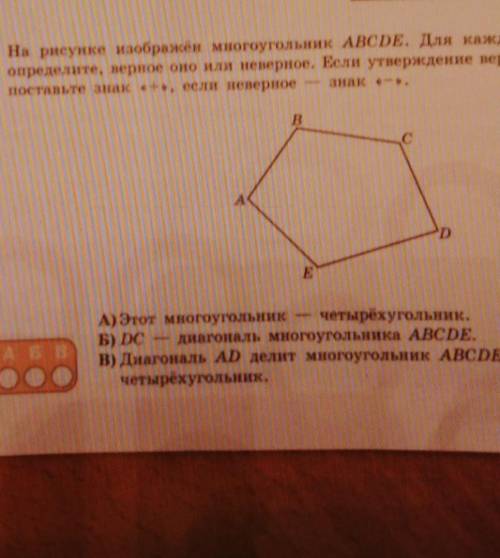
На рисунке изображен многоугольник ABCDE. Для каждого утверждения
определите, верное оно или неверное. Если утверждение верное, то в таблицу
поставьте знак не, если неверное и анан ер
ТЕМИ
МІН
А) Этот многоугольник четырехугольника
Б) DC - диагональ многоугольника ABCDE.
В) Диагональ А2 делит многоугольник ABCDE на треугольник и
четырехугольник.
Другие вопросы по теме Математика
Популярные вопросы
- Напряжение источника равно 3,6 В. Сопротивления резисторов равны 2 и...
2 - Мне нужно сочинение на тему волшебная сила на море не больше одного листа...
3 - Среднее арифметическое четырех натуральных чисел составляет 43 1/2, а...
1 - Адамзат қиялы - Шындық туралы эссе 5-6 сөйлем.5-класс . ...
1 - Установите соответствие понятий и определений...
1 - Установіть відповідність між елементами грошової маси та грошовими агрегатами,...
1 - Чем отличаются зонные структуры проводника и полупроводника?...
2 - До ть будь ласка яке словосполучення зробити зі словом клас ?...
2 - Каковы нравы чиновников города?...
3 - В урне 6 белых шар(-ов, -а), 10 чёрных, 14 в полоску и 6 в клетку. Определи...
3
А) Этот многоугольник четырехугольник.
Чтобы определить, является ли многоугольник ABCDE четырехугольником, нужно посчитать количество его сторон. Если количество сторон равно 4, то многоугольник является четырехугольником. На рисунке у нас видно, что многоугольник ABCDE имеет 5 сторон (AB, BC, CD, DE, EA). Следовательно, это утверждение неверно.
Б) DC - диагональ многоугольника ABCDE.
Диагональ - это отрезок, соединяющий две несоседние вершины многоугольника. На рисунке видно, что отрезок DC соединяет вершины D и C, которые не являются соседними. Поэтому DC действительно является диагональю многоугольника ABCDE. Это утверждение верно.
В) Диагональ А2 делит многоугольник ABCDE на треугольник и четырехугольник.
Чтобы определить, является ли диагональ А2 делителем многоугольника ABCDE на треугольник и четырехугольник, нужно проверить, пересекает ли она стороны многоугольника только внутри фигуры. На рисунке видно, что диагональ А2 (отрезок AC) пересекает сторону CD, но не пересекает сторону DE. Поэтому диагональ А2 делит многоугольник ABCDE на два треугольника (ABC и ADE) и один четырехугольник (CDEA). Это утверждение верно.
Таким образом, ответы на утверждения:
А) неверное (ан),
Б) верное (вер),
В) верное (вер).